Statische Analysen von Balken und Stäben” subtitle: “mittels der Finite-Elemente-Simulationsmethode mit SOLIDWORKS
Stabkonstruktionen werden in verschiedenen Formen überall eingesetzt. Typischerweise werden sie bei der Konstruktion von Kränen, Fachwerkauslegern, Fernmeldetürmen, Masten, Strommasten, Dächern, Brücken usw. eingesetzt.
Aus der Sicht der technischen Leistungsanalyse werden statische Analysen von Balken und Stäben mit folgenden Zielen durchgeführt:
- Bestimmung der Schnittgrößen und damit der Spannungen, die sich in den Stäben entwickeln.
- Bewertung der axialen Verformung, die die Stäbe bei Belastung erfahren.
Die folgenden technischen Punkte werden bei der Rechneranalyse von Stäben häufig berücksichtigt:
- Die Stäbe eines Fachwerks sind gerade und haben gleichmäßige Querschnitte.
- Die Enden eines einzelnen Stabes des Fachwerks sind mit den Enden anderer Stäbe über reibungsfreie Stifte verbunden. In der Praxis können solche Verbindungen durch Nieten/Schrauben/Kugelgelenke oder durch Schweißen an ein Knotenblech hergestellt werden.
- Kräfte und Stützen werden nur an den Verbindungsstellen eines Stabes eingeleitet.
Strategien für die Analyse von Stäben
In diesem Abschnitt werden die strukturellen Details und die Modellierungsstrategien für die Simulation von Stabkonstruktionen beschrieben. Außerdem werden die wichtigsten Merkmale des Stabelements innerhalb der SOLIDWORKS Simulation Bibliothek hervorgehoben.
Strukturelle Einzelheiten
Unabhängig davon, welche Form ein Stab hat, wird ein einheitlicher Satz von Parametern für seine Analysen verwendet. Die folgenden technischen Informationen werden benötigt, bevor man sich an die Analyse wagt:
- Die Abmessungen des Stabes:
- Die Details des Querschnitts
- Die geometrische Länge der einzelnen Stäbe
- Die Orientierungswinkel der Stäbe
- Die Materialeigenschaften der Stabelemente
- die Lasten, die auf bestimmte Verbindungen des Stabes wirken
- die Abstützung des Stabes zur Vermeidung von Starrkörperbewegungen
Modellierungsstrategie
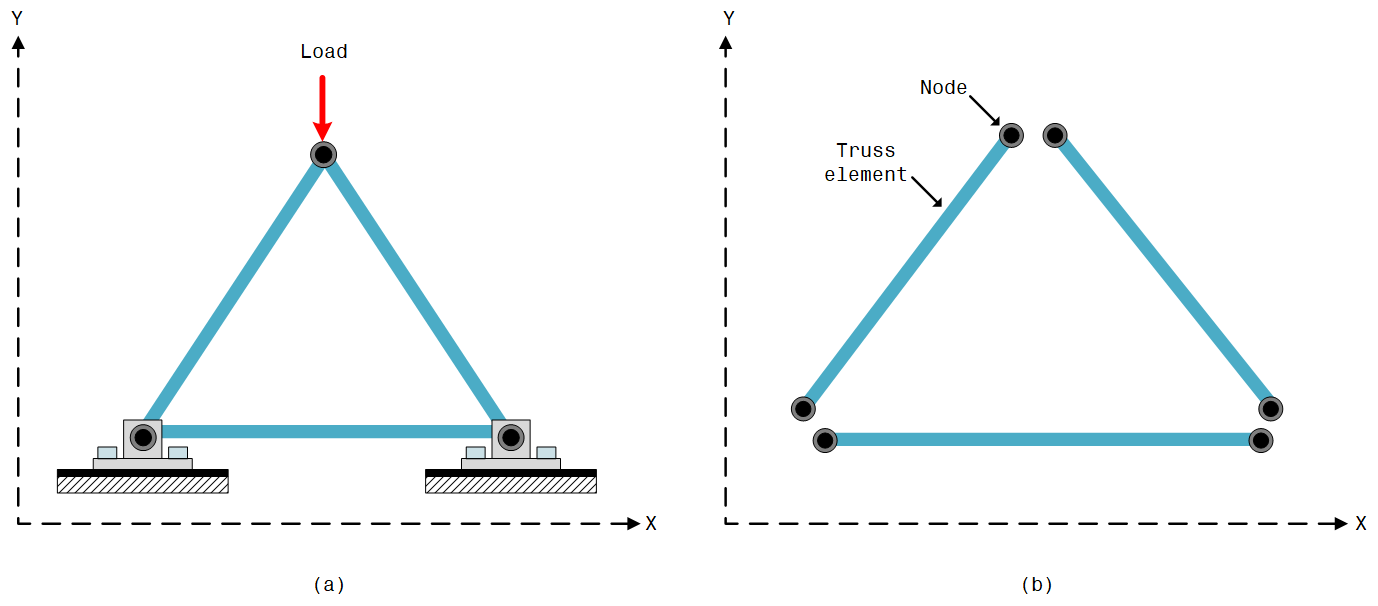
Bei der Analyse von Stabkonstruktionen mit Hilfe der Finite-Elemente-Simulationsmethode besteht eine grundlegende Strategie darin, eine Struktur wie die in Abbildung 1 (a) dargestellte zu nehmen, sie in ihre einzelnen Elemente zu zerlegen (Abbildung 1 (b)) und dann jedes Element als Stabelement zu behandeln. Auf diese Weise wird ein ganzes Tragwerk, das sich aus verschiedenen Stäben zusammensetzt, durch das kollektive Verhalten der einzelnen Stabelemente dargestellt.
Die wichtigsten Schritte bei der statischen Analyse von Stäben sind:
- Modellierung der Skelettstruktur (Skelettanordnung) des Stabes oder einer Sammlung von Stäben in der SOLIDWORKS Modellierungsumgebung.
- Umwandlung der Skelettstruktur in ein Schweißkonstruktionsprofil in der SOLIDWORKS-Modellierungsumgebung, wobei das Schweißkonstruktionsmodell in ein Finite-Elemente-Modell umgewandelt wird (im SOLIDWORKS-Simulations-Fenster).
- Durchführung der Analyse, um die Ergebnisse zu erhalten (im SOLIDWORKS Simulation-Fenster).
PROBLEM 1: Durchführung einer statischen Analyse für einen Kran
Problembeschreibung
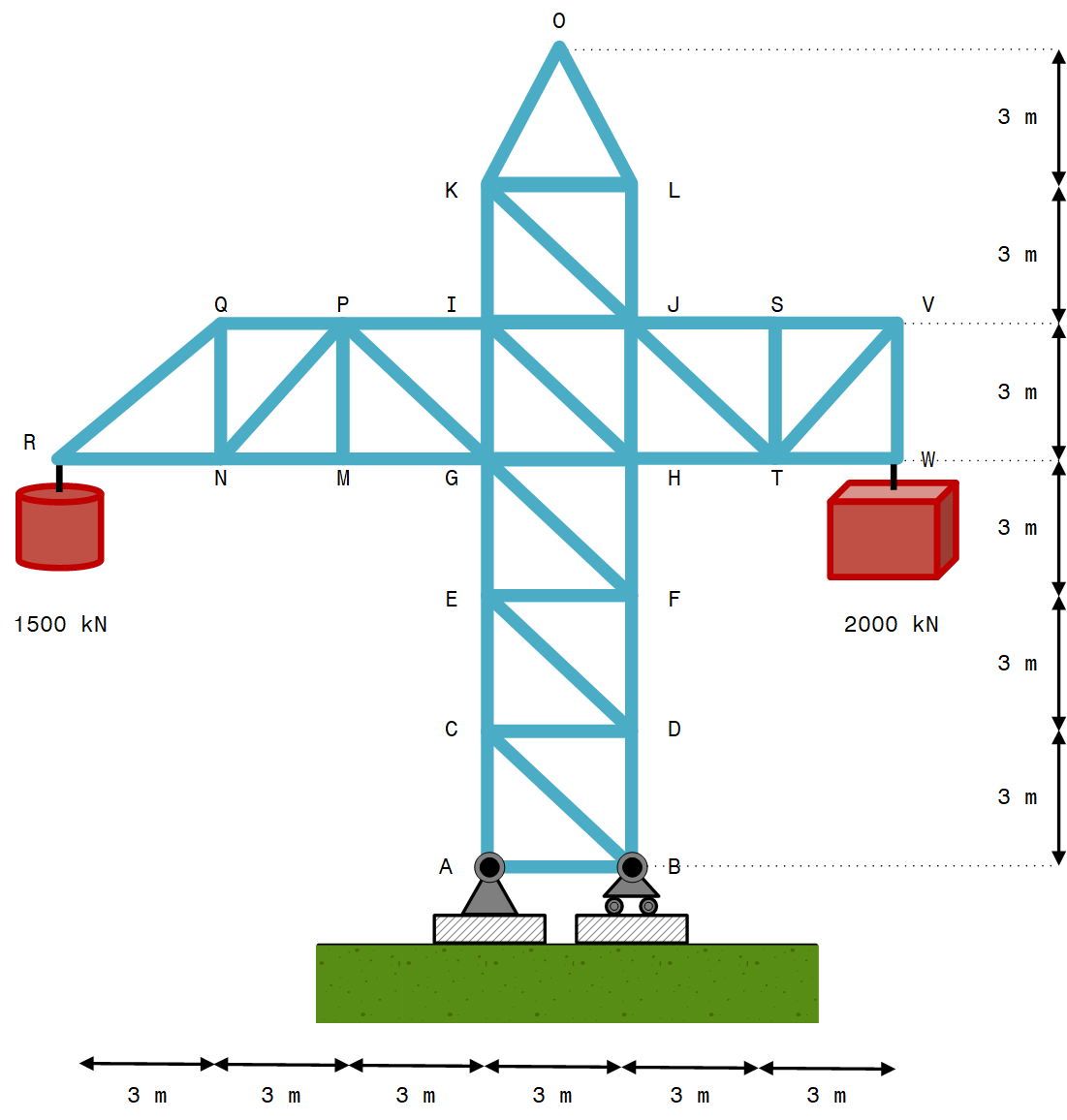
Analyse der strukturellen Leistung eines Krans, der für die räumliche Positionierung schwerer Objekte auf einer Mega-Baustelle verwendet wird. Eine 2D-Darstellung des zu untersuchenden Krans ist in Abbildung 2 dargestellt. Der Kran wird an den Punkten $R$ und $W$ mit Gewichten von $1500 \ kN$ bzw. $2000 \ kN$ belastet.
Es wird angenommen, dass die Teile des Krans aus legiertem Stahlrohr mit einem Elastizitätsmodul $E$ von $210 \ GPa$ bestehen. Die Stäbe haben den gleichen Querschnitt mit einem Außen- und Innendurchmesser von $200 \ mm$ bzw. $80 \ mm$.
Ziele
Beantwortung der folgenden Fragen mit Hilfe der SOLIDWORKS-Simulation:
- Wie groß ist die maximale resultierende Verformung des Stabes bei der Einwirkung der Lasten?
- Wie ist die Verteilung des Sicherheitsfaktors der Stäbe des Krans bei Belastung?
- Wie hoch ist die innere Kraft/Spannung, die sich im Stab $IH$ entwickelt?
Lösung
- Teil A - Erstellung der Skizze des geometrischen Modells
- Teil B - Umwandlung des Strukturskelettmodells in ein Strukturprofil
- Teil C - Erstellung der Simulationsstudie
- Teil D - Prüfung der Ergebnisse
Teil A - Erstellung der Skizze des geometrischen Modells
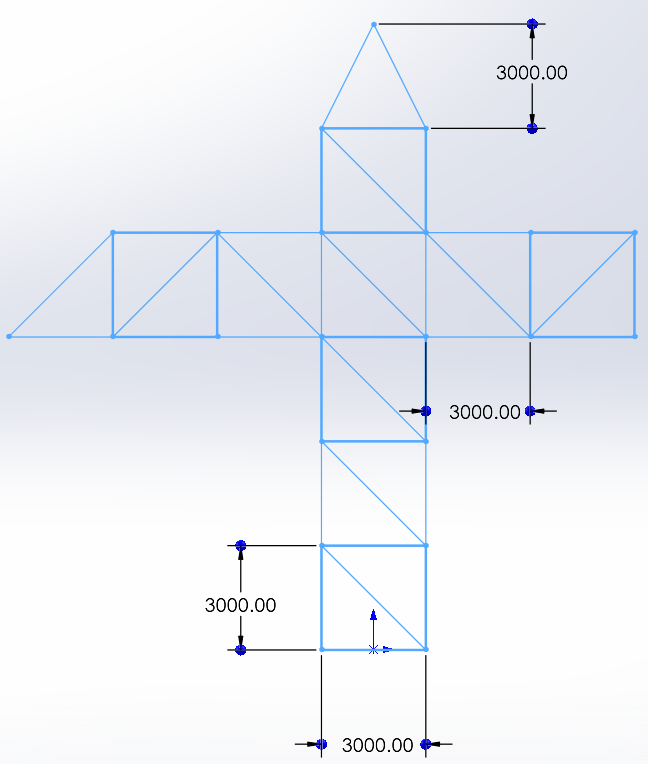
Zunächst wird ein Modell der Kranstruktur (Skelettskizze des Modells) erstellt, indem die Linien, die die Geometrie des Krans beschreiben, mit dem Skizzierwerkzeug Linie skizziert werden. Die verwendete Maßeinheit ist das MMGS (Millimeter, Gramm und Sekunde)-Einheitensystem. Die fertige Skizze sieht aus wie der Screenshot in Abbildung 3.
Diese erstellte Skizze ist nur eine Reihe von Linien ohne Volumeneigenschaften. Als solche kann sie nicht für Strukturanalysen verwendet werden. Im nächsten Schritt wird das skizzierte linienbasierte Modell in ein Strukturmodell mit Volumeneigenschaft umgewandelt.
Teil B - Umwandlung des Strukturskelettmodells in ein Strukturprofil
Der nächste Schritt besteht darin, die im vorangegangenen Abschnitt erstellten Linienskizzen in ein Strukturmodell umzuwandeln. Dies geschieht mit Hilfe einer speziellen Funktion in SOLIDWORKS, dem Werkzeug Schweißkonstruktionen, das die Umwandlung von Linien ohne Volumeneigenschaften in Strukturelemente mit Volumeneigenschaften ermöglicht, die für eine realistische technische Simulation geeignet sind. Dies geschieht durch Vorgabe der Querschnittsdetails für die skizzierten Linien.
Dazu wird der Befehl Strukturbauteil aus der Symbolleiste Schweißkonstruktionen verwendet und im Fenster PropertyManager des Strukturbauteils werden die folgenden Optionen ausgewählt:
- Norm: iso
- Typ: Rohr
- Größe: $33,7 \times 4,0$, - was sich auf ein Rohr mit einem Außendurchmesser von $33,7 \ mm$ und einer Dicke von $4 \ mm$ bezieht.
Dann werden sechs Gruppen von Linien ausgewählt (ohne Anwendung der Eckenbehandlung). Die für jede Gruppe auszuwählenden Linienreihen sind in Abbildung 4 (a-f) dargestellt.
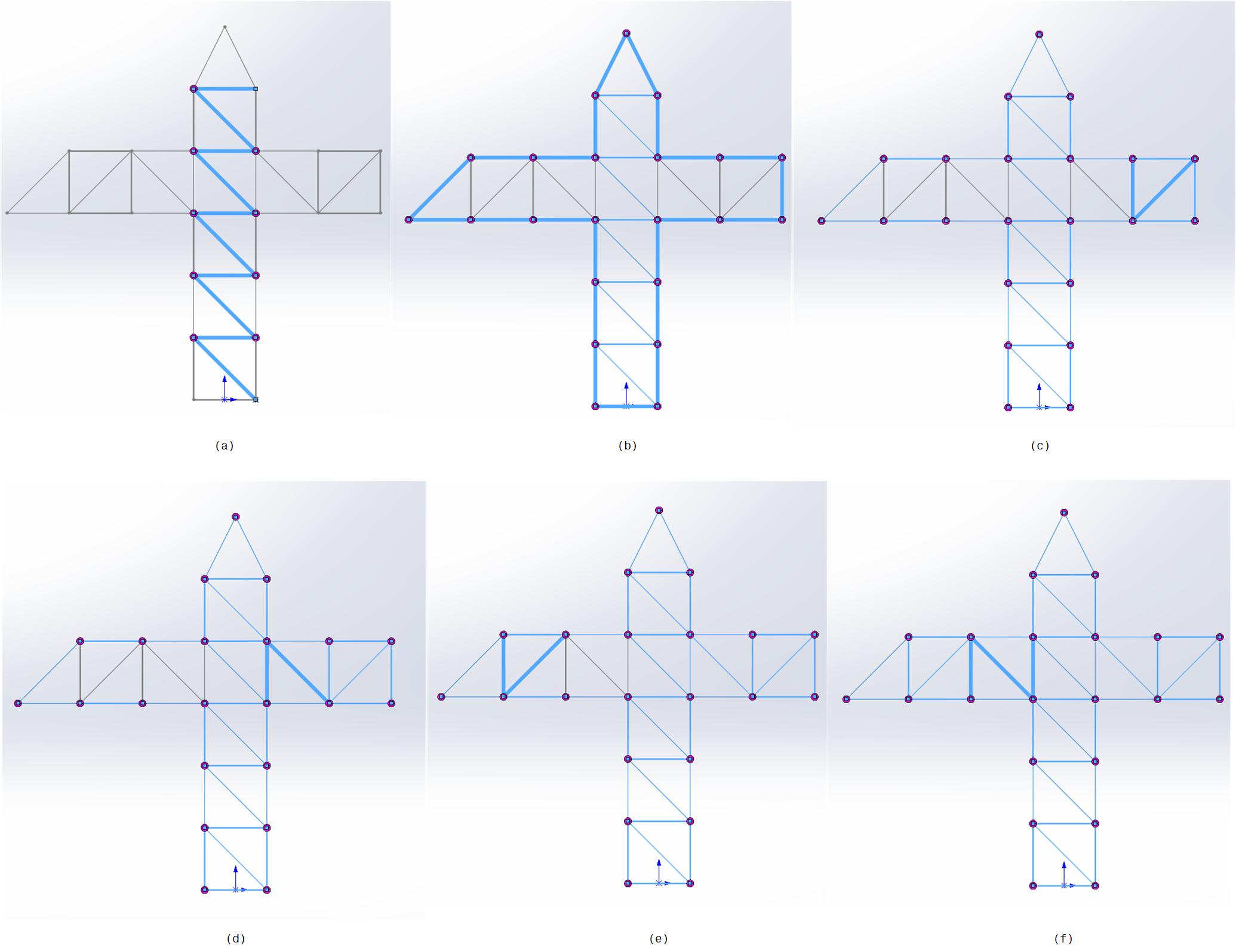
Nach Abschluss der oben genannten Schritte erscheint der FeatureManager mit einigen zusätzlichen Elementen, wie z. B. dem Element Zuschnittliste (41), das anzeigt, dass es insgesamt $41$ Schweißteile gibt, aus denen die Kranstruktur besteht, und dem Element Rohr, das der Hauptzweig der Sammlung von extrudierten Körpern ist, die die $41$ Strukturteile des Krans darstellen.
Der verwendete Querschnitt aus der Schweißkonstruktionsbibliothek entspricht nicht dem, der in der Problembeschreibung angegeben ist. Um die Abmessungen dieses Querschnitts zu ändern, wird die Skizze im Element Rohr im FeatureManager von Abbildung 5a auf die gewünschten Abmessungen (Abbildung 5b) geändert.
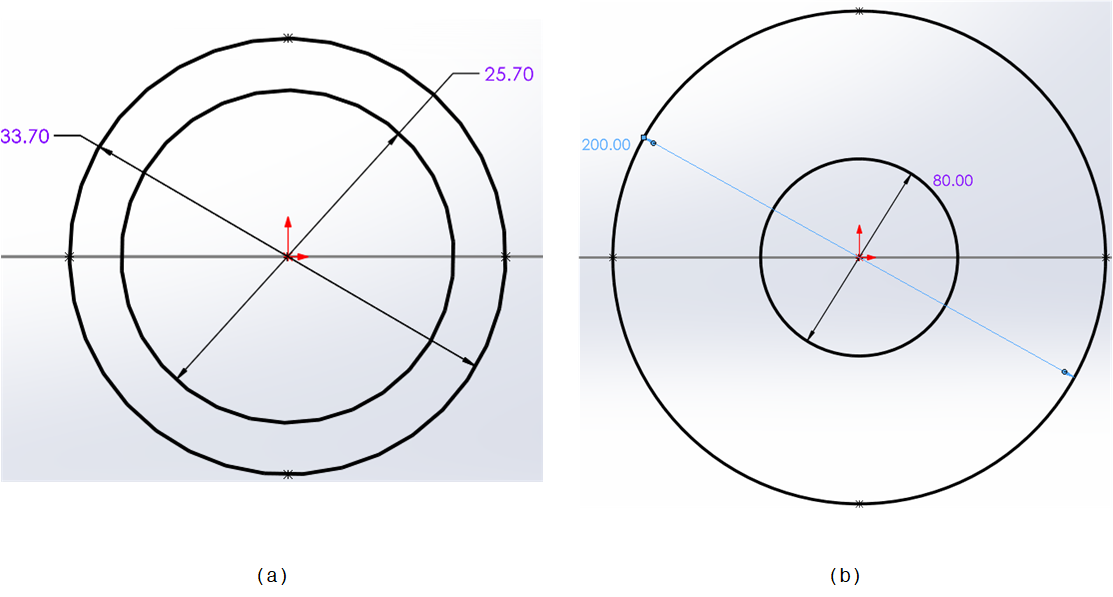
Teil C - Erstellung der Simulationsstudie
In diesem Abschnitt wird eine statische Analyse der Kranstruktur durchgeführt. Dazu werden nach dem Aktivieren der Simulationsregisterkarte und dem Anlegen einer neuen Studie das Material für die Bauteile spezifiziert, das Stabelement, die Einspannungen/Lasten angewandt und schließlich der Vernetzungsprozess eingeleitet.
$\quad$ 1. Aktivierung der Registerkarte Simulation und Erstellung einer neuen Studie
In diesem Schritt wird nach dem Aktivieren der Registerkarte “Simulation” eine neue Studie mit dem Namen “Crane Analysis” (Krananalyse) erstellt und die Option “Statische Analyse” in den Eigenschaften von “Allgemeine Simulation” im Bereich “PropertyManager” ausgewählt. Daraufhin wird die Studien-Baumstruktur “Simulation” gestartet, Verbindungen werden an den Verbindungspunkten zwischen den Stabelementen eingefügt und die Simulation-Befehle werden verfügbar, wie in Abbildung 6 dargestellt.
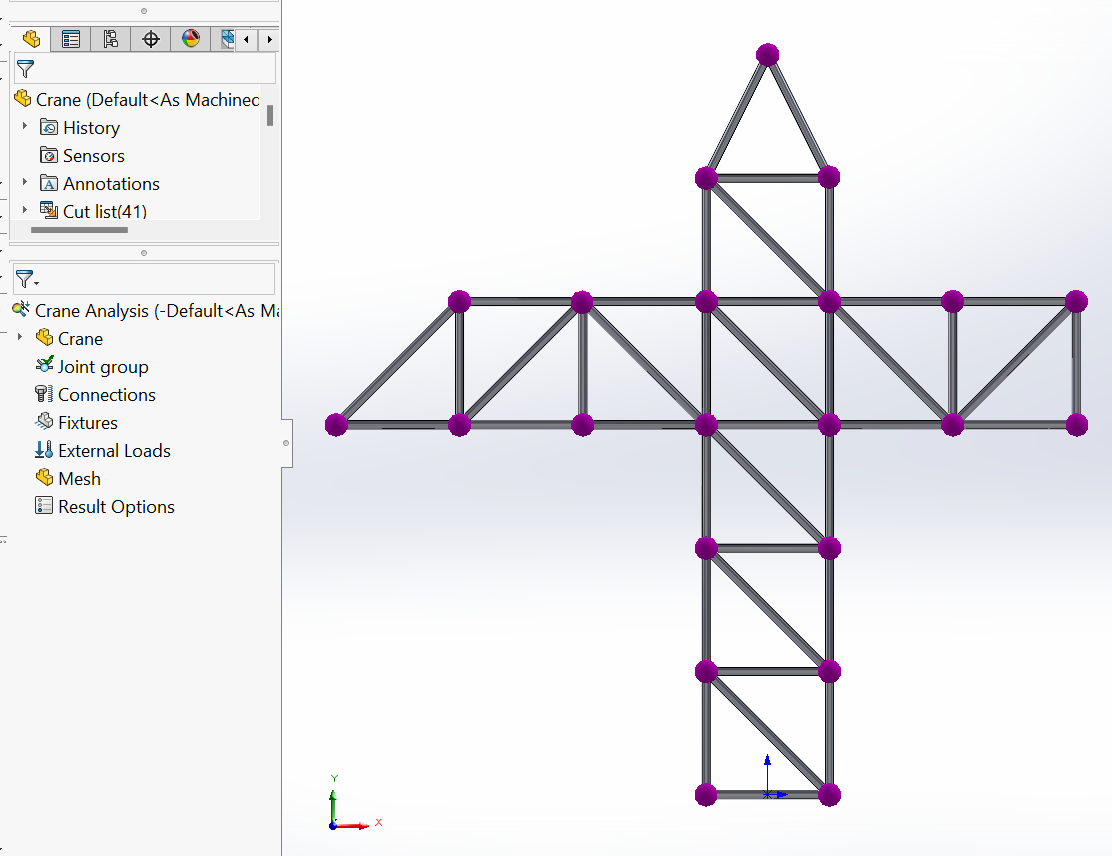
$\quad$ 2. Hinzufügung einer Materialeigenschaft
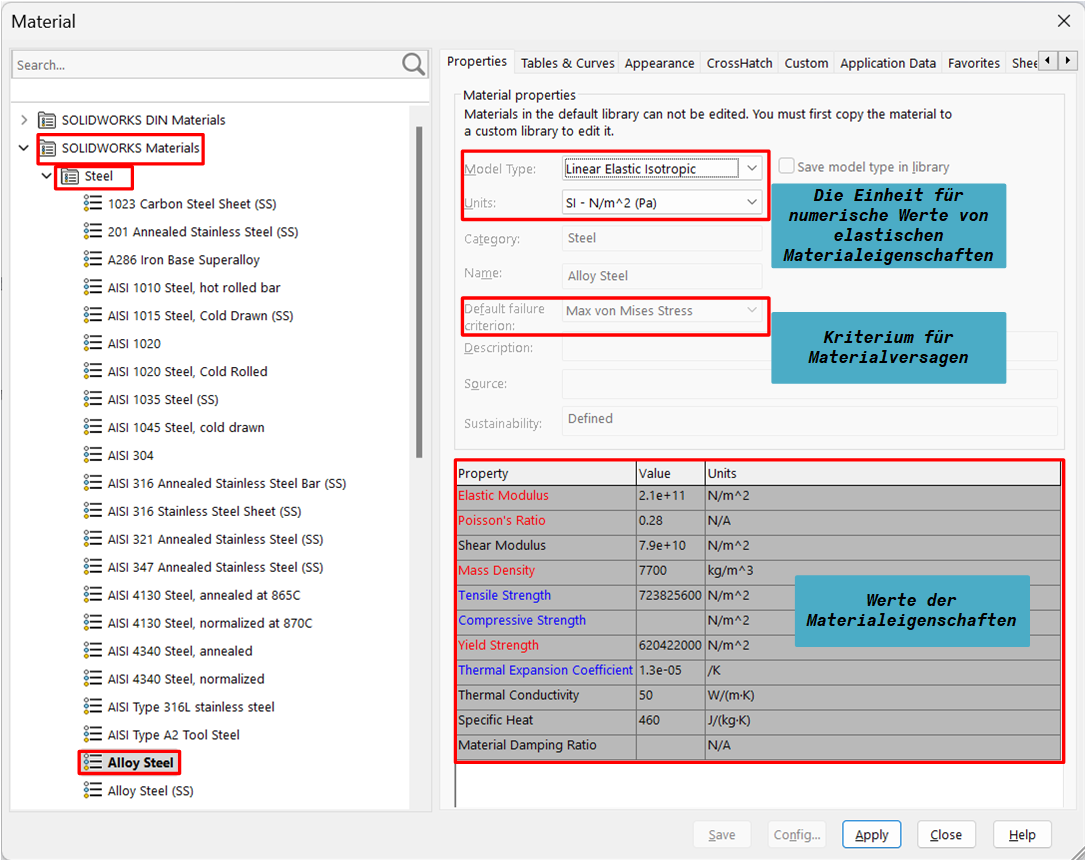
Es wird davon ausgegangen, dass jedes Element des Krans aus demselben Material besteht. Um das Material auf die Stäbe anzuwenden, wird die Materialdatenbank aufgerufen und in diesem Fall “legierter Stahl” aus dem Unterordner “Stahl” ausgewählt.
Die linke Seite des Dialogfelds “Material “, Abbildung 7, enthält eine Baumstruktur der verfügbaren Materialtypen und Materialien, d. h. eine Materialdatenbank, die ein mehrstufiges Verzeichnis ist. An der Spitze der Baumstruktur befindet sich der Hauptordner SOLIDWORKS Materialien, gefolgt von Unterordnern, die jeweils Materialien enthalten, die zur gleichen Familie gehören. Auf der Registerkarte Eigenschaften sind die Namen der Materialeigenschaften entweder in schwarzer, blauer oder roter Schriftfarbe dargestellt. Im Allgemeinen sind die Namen der Materialeigenschaften in roter Farbe diejenigen, die für statische Analysen erforderlich sind. Ein Materialversagenskriterium (Max von Mises Spannung) und ein Linear elastisches isotropes Materialmodell sind für das ausgewählte Material vordefiniert.
Ein Material wird als isotrop bezeichnet, wenn seine Eigenschaften nicht mit der Richtung variieren. Isotrope Materialien haben in allen Richtungen den gleichen Elastizitätsmodul, die gleiche Poissonzahl, den gleichen Wärmeausdehnungskoeffizienten, die gleiche Wärmeleitfähigkeit usw.
$\quad$ 3. Wechsel von einem Balkenelement zu einem Stabelement
Standardmäßig behandelt SOLIDWORKS Simulation ein Strukturbauteil, das mit dem Schweißkonstruktionswerkzeug erstellt wurde, während der Analyse als Balkenelement. In diesem Fall ist jedoch ein Stabelement erforderlich. Der Unterschied besteht darin, dass ein Balkenelement axialen, Biege- und Torsionsbelastungen standhält, während ein Stabelement nur axialen Belastungen standhalten kann. Daher werden alle Strukturbauteile, die sich in den Unterordnern des Ordners “Schnittliste” im “FeatureManager” befinden, von Balken in Stäbe umgewandelt, indem ihre Definition mit der Option “Definition bearbeiten” von Balken in Stab umgewandelt wird.
$\quad$ 4. Anbringen einer Einspannung
Eine Einspannung ist eine Beschränkung, die auf Strukturen angewendet wird, um die Bewegung ihres Gelenks/Segments zu begrenzen, wenn Lasten aufgebracht werden. Für diese Analyse werden drei Sätze von Einspannungen auf das Strukturmodell des Krans angewendet:
- Eine Einspannung, die die normale Bewegung aller Gelenke (d. h. der Eckpunkte des Krans) zur Vorderansicht verhindert. Dies ist notwendig, da in diesem Fall eine planare (2D) Analyse des Krans durchgeführt wird. Im Falle einer 3D-Analyse ist dies jedoch nicht erforderlich.
- Eine Einspannung, die Bewegungen in horizontaler und vertikaler Richtung am Gelenk $A$ verhindert (da das Gelenk $A$ ein festes Auflager hat).
- Eine Einspannung, die die Bewegung in vertikaler Richtung am Gelenk $B$ verhindert (da dieses Gelenk durch ein Rollengelenk abgestützt ist).
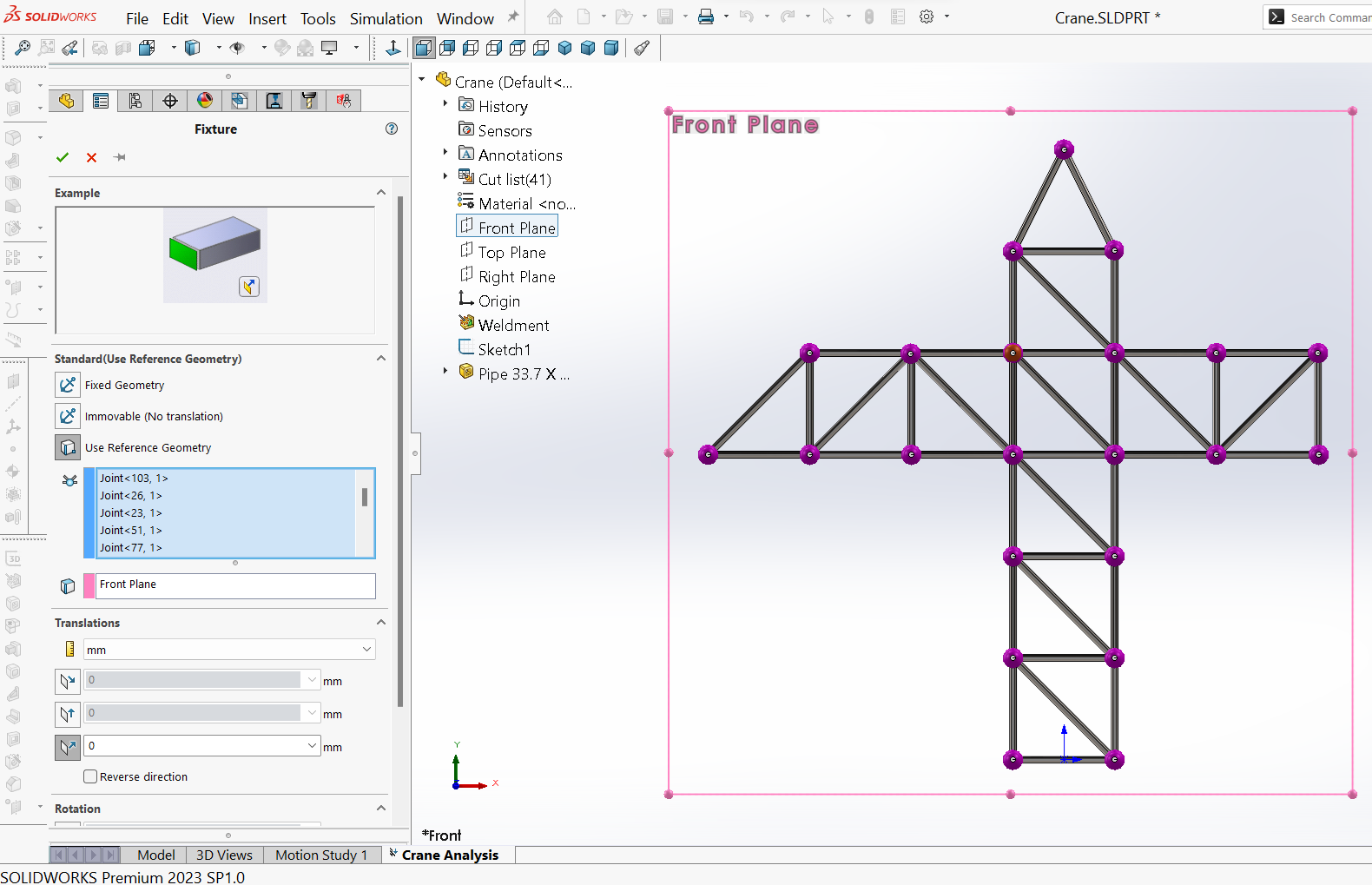
Um die $Z$-Bewegung aller Knoten einzuschränken, d.h. allen Knoten entlang der $Z$-Achse eine Translationsbewegung von Null aufzuerlegen, was die spätere Durchführung einer ebenen Analyse gewährleistet, wird in der Studien-Baumstruktur “Simulation” die Option Einspannungen mit der rechten Maustaste angeklickt und Fixierte Geometrie ausgewählt. Dann wird unter Fixture PropertyManager und im Abschnitt Standard die Option Verwenden einer Referenzgeometrie gewählt, um die Einspannungen anzuwenden. Alle Verbindungen im Grafikfenster werden nacheinander ausgewählt. Die Ebene vorne wird aus dem FeatureManager als Bezugsebene für die Anwendung von Beschränkungen ausgewählt (im Feld für die Referenzebene vermerkt). Dann wird im Abschnitt Verschiebungen das Kästchen für Normal zur Ebene ausgewählt. Diese Optionen sind in Abbildung 8 dargestellt.
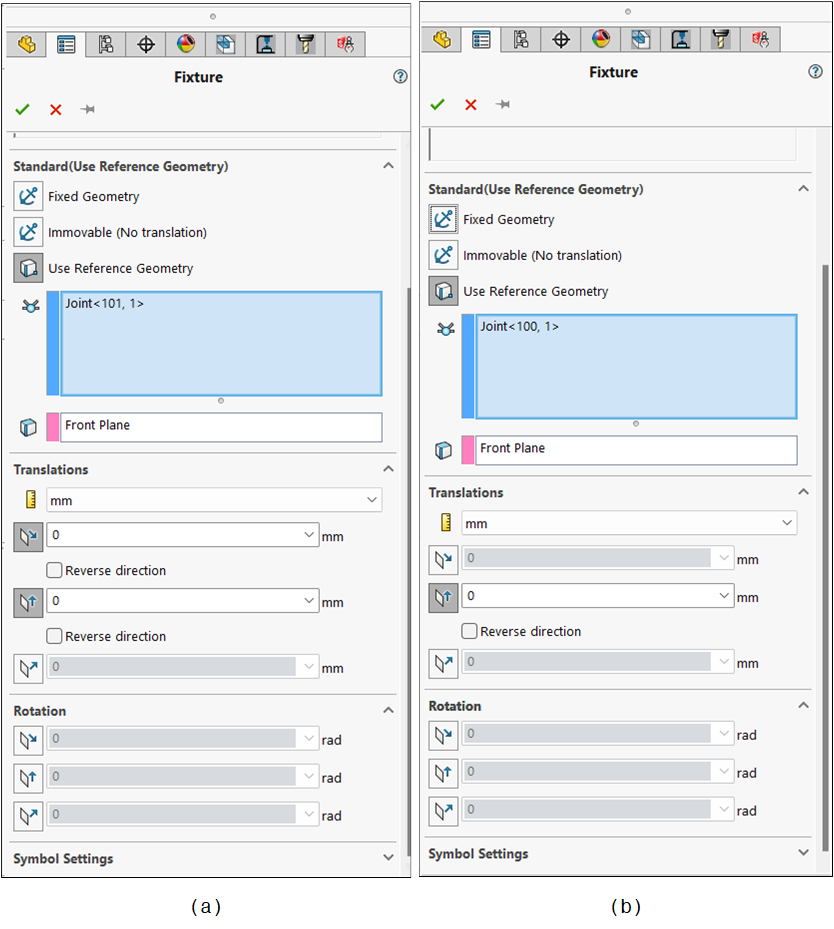
Dann werden die Einspannungen an den Verbindungen $A$ und $B$, die sich beide am Fuß des Krans befinden, aufgebracht, indem die Einspannungen an den Knoten $A$ und $B$ in ähnlichen Schritten wie im vorigen Abschnitt beschrieben aufgebracht werden, entsprechend den in Abbildung 9 (a-b) gezeigten Einstellungen.
Für die Verbindung $A$ konnte auch die Vorrichtung Nicht verschiebbar (keine Translation) verwendet werden; sie erfüllt die gleiche Funktion wie die Verwenden einer Referenzgeometrie. Für die Verbindung $B$ wurde die Bewegung nur in der vertikalen Richtung eingeschränkt, um das Verhalten eines horizontalen Rollenträgers nachzubilden.
$\quad$ 5. Aufbringen externer Lasten
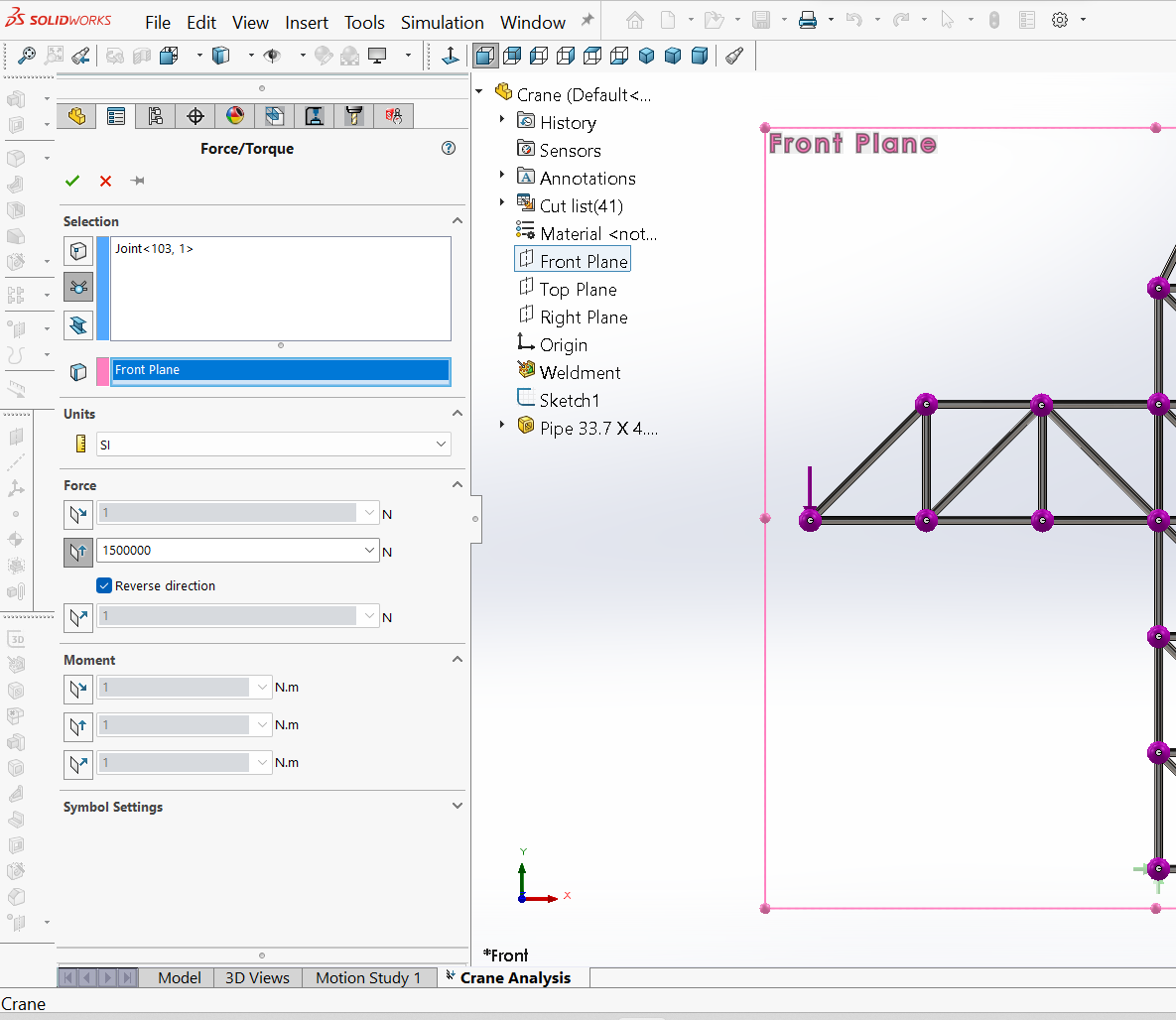
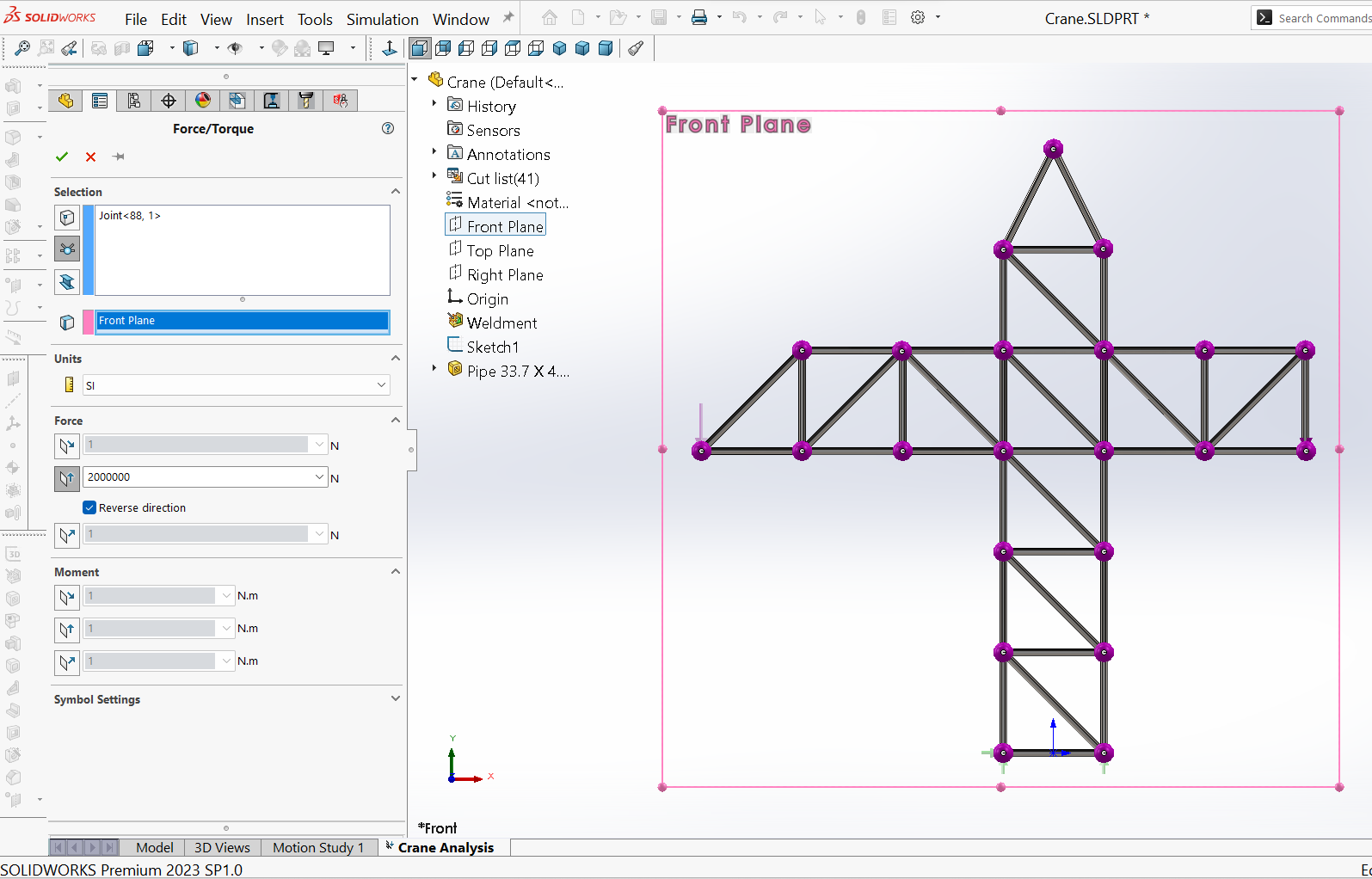
In SOLIDWORKS Simulation können verschiedene Arten von Lasten verwendet werden. In diesem Fall sind Nutzlastgewichte erforderlich, die durch zwei vertikale Kräfte an den Verbindungen $R$ und $W$ dargestellt werden. Die Lasten werden durch Klicken mit der rechten Maustaste auf den Befehl Externe Lasten in der Studien-Baumstruktur “Simulation” und Auswahl von Kraft angewendet. Dann im PropertyManager Kraft, der unter Auswahl erscheint, auf das Symbol Verbindungen klicken und dann die Verbindung (hier: $R$ und dann “W”) im Grafikfenster auswählen und die Optionen für die Verbindung “R”, wie in Abbildung 10 gezeigt, wo eine Kraft von $1500 \ kN$ aufgebracht wird, und für die Verbindung “W”, Abbildung 11, wo eine Kraft von $2000 \ kN$ aufgebracht wird, auswählen.
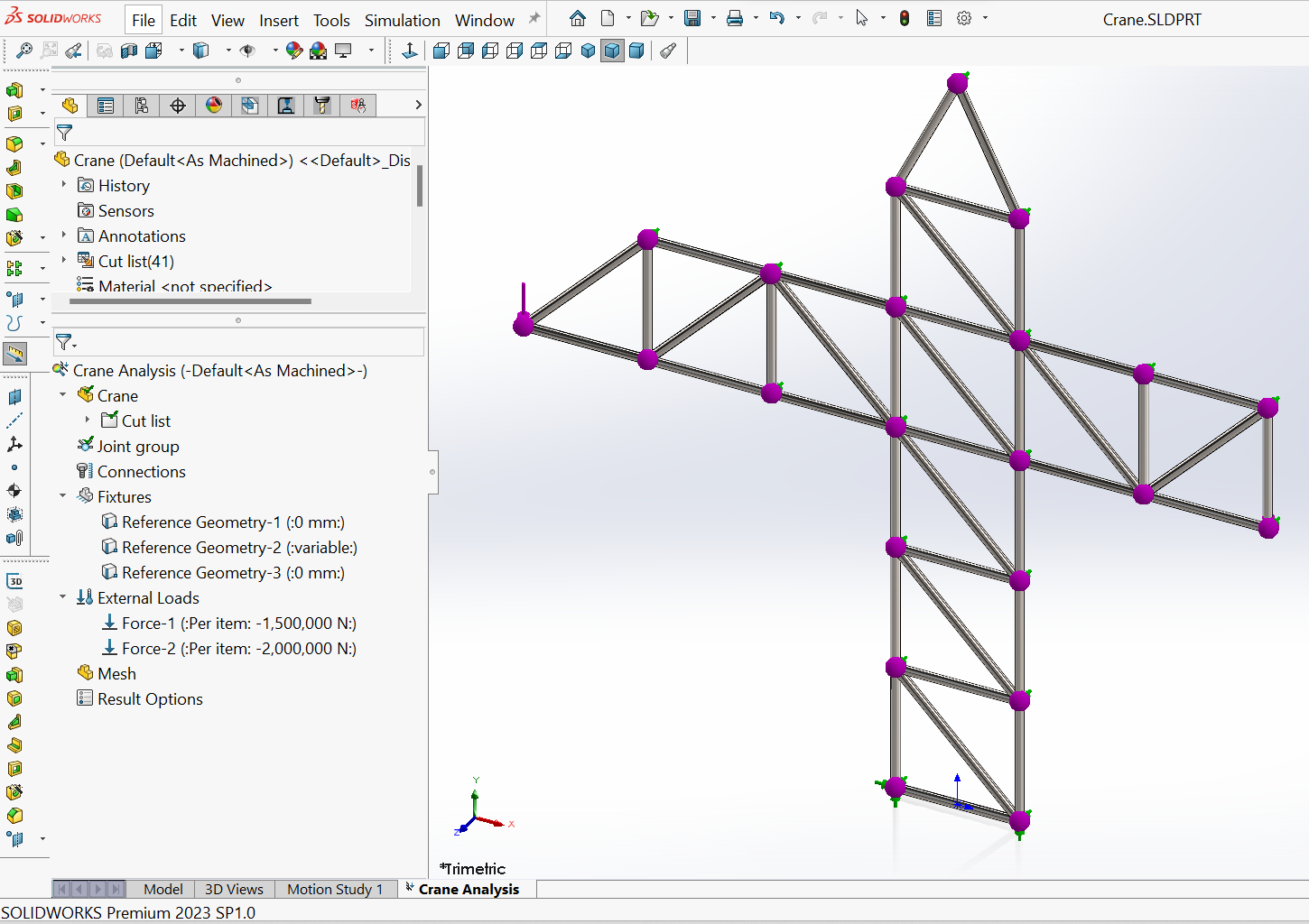
Nach der Anwendung der Kräfte sieht das Modell im Grafikfenster wie in Abbildung 12 dargestellt aus.
$\quad$ 6. Vernetzung
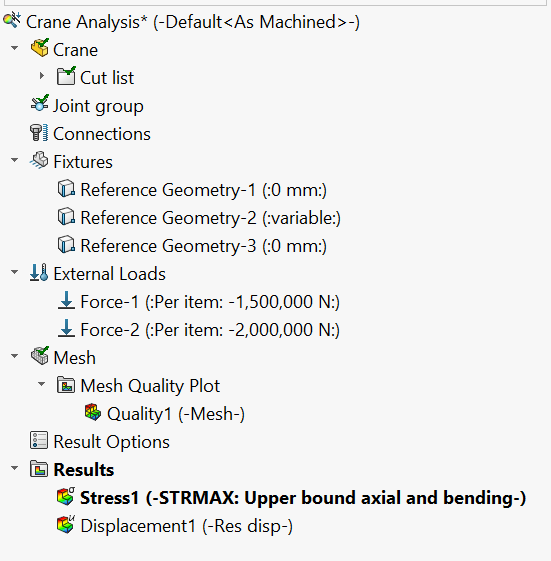
Die Vernetzung wird mit dem Befehl Vernetzen und Durchführen erstellt, der die Vernetzung und die Durchführung der Analyse in einem einzigen Schritt kombiniert. Nach Abschluss der Vernetzung erscheint der Studienbaum wie in Abbildung 13 dargestellt.
Teil D - Prüfung der Ergebnisse
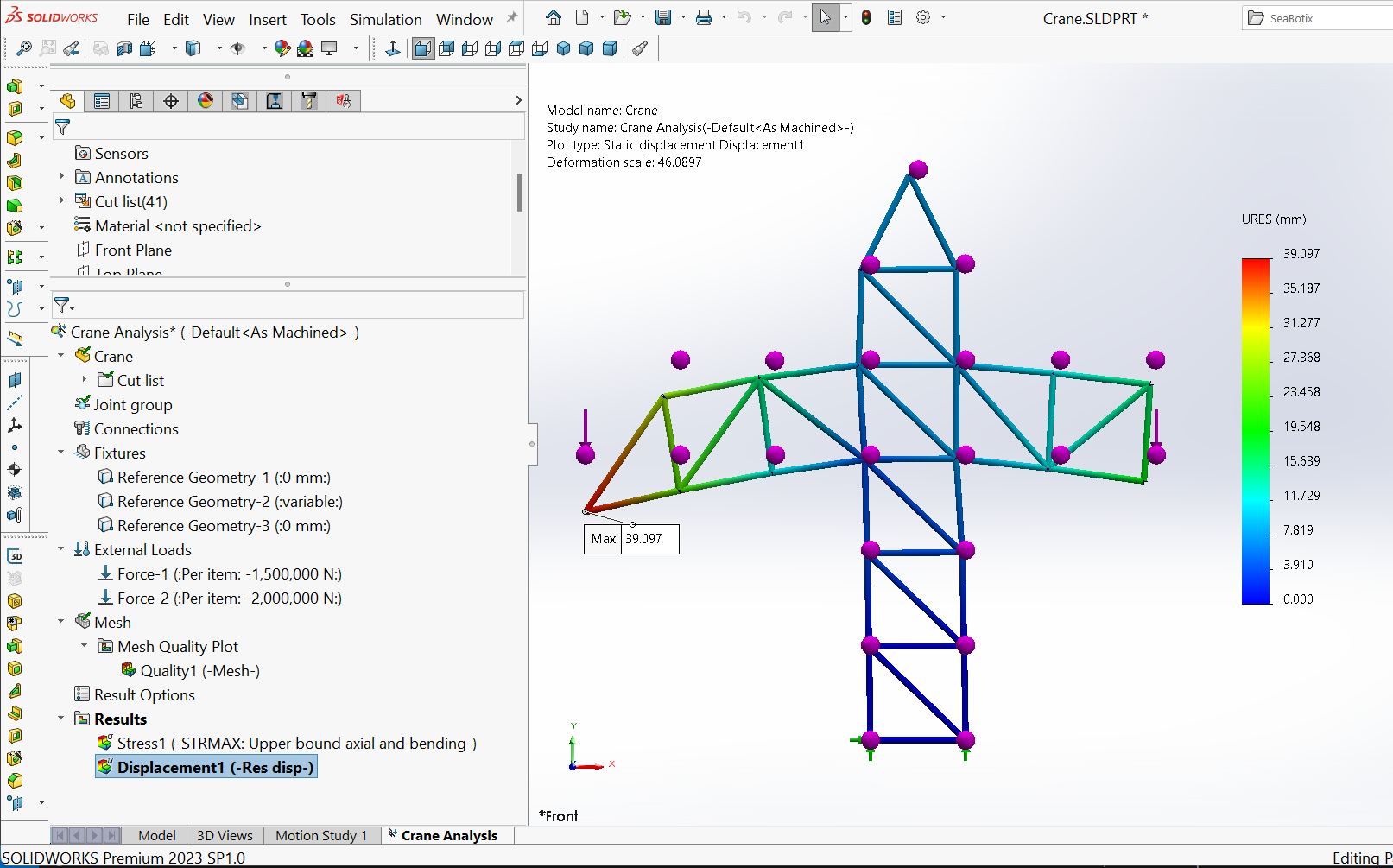
Wenn SOLIDWORKS für statische Studien verwendet wird, berechnet es im Allgemeinen unter anderem die Verschiebungen (Abbildung 14) an den Verbindungen oder Knoten der Struktur, den Sicherheitsfaktor (Abbildung 15), die Rückwirkungskräfte an den Auflagerpunkten, die Dehnungen/Spannungen an einem Element/Knoten usw.
Die maximale resultierende Verformung
Abbildung 14 zeigt, dass bei einer kombinierten Last von $3500 \ kN$, die auf den Kran wirkt, die maximale Verformung des Gelenks $R$ $39.097 \ mm$ beträgt. Da ein Stabelement an seinem Knoten drei translatorische Verschiebungsfreiheitsgrade besitzt, bezieht sich die resultierende Verschiebung auf die vektorielle resultierende Verschiebung.
Der Sicherheitsfaktor
Die Berechnung des Sicherheitsfaktors basiert auf bestimmten Versagenskriterien. SOLIDWORKS Simulation bietet vier Versagenskriterien:
- Maximales von-Mises-Spannungskriterium
- Maximales Schubspannungskriterium
- Mohr-Coulomb-Spannungskriterium
- Maximales Normalspannungskriterium (für Verbundstoff-Schalen)
Hohe Sicherheitsfaktoren in einem Bereich zeigen an, dass Sie in diesem Bereich Materialeinsparungen vornehmen können. Viele Codes erfordern einen minimalen Sicherheitsfaktor zwischen $1,5$ und $3$.
- Ein Sicherheitsfaktor unterhalb von $1$ an einer Position zeigt an, dass das Material an dieser Stelle versagt hat.
- Ein Sicherheitsfaktor von $1$ an einer Position zeigt an, dass das Material an dieser Stelle gerade begonnen hat, zu versagen.
- Ein Sicherheitsfaktor oberhalb von $1$ an einer Position zeigt an, dass das Material an dieser Stelle sicher ist.
Abbildung 15 zeigt die Verteilung des Sicherheitsfaktors für den Kran bei Aufbringung der Last. Hier wird das Maximum Von-Mises Versagenskriterium verwendet, das in der Datenbank der Materialeigenschaften angegeben ist.
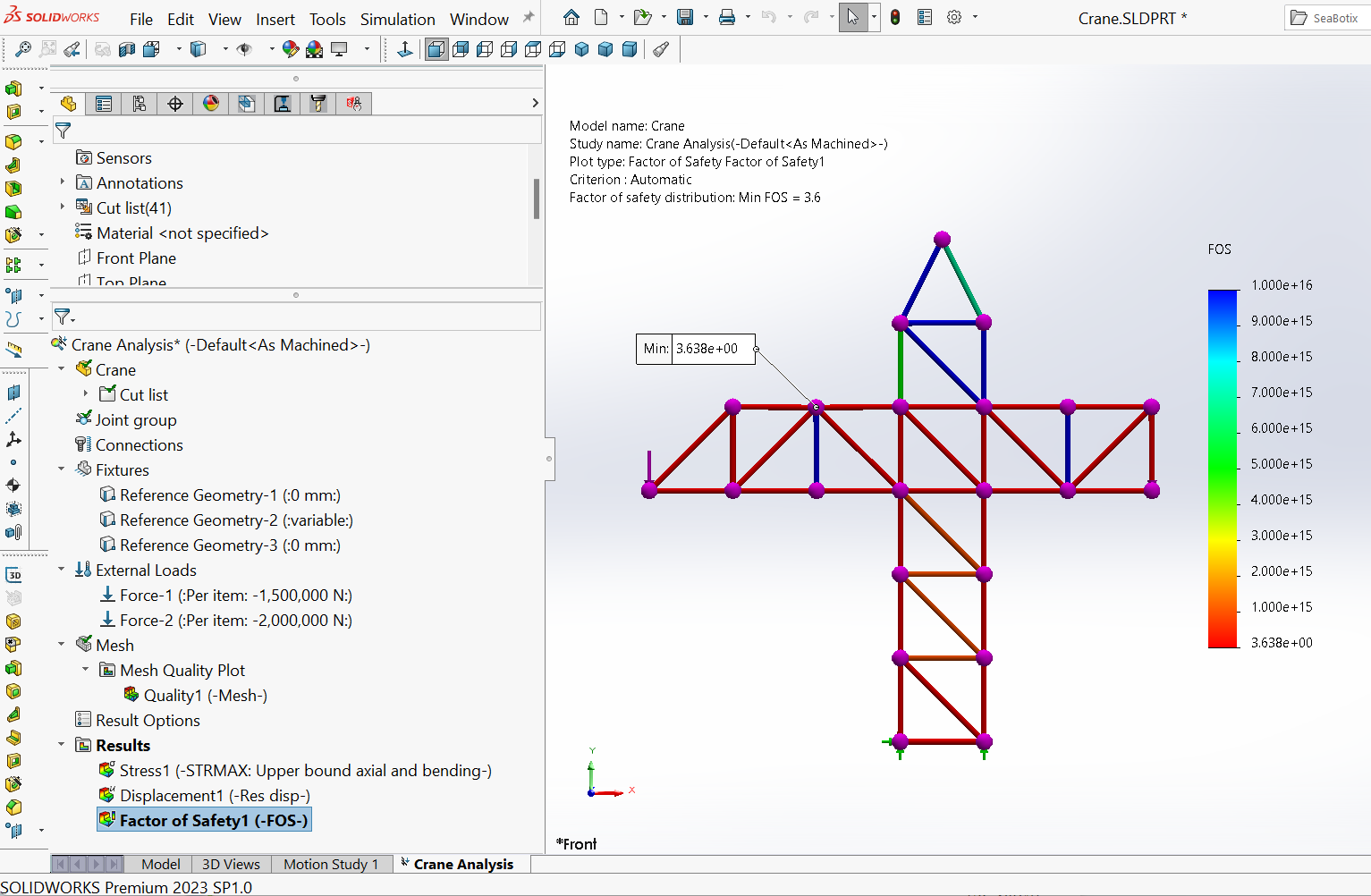
Die Axialkraft/Spannung für den Stab $IH$
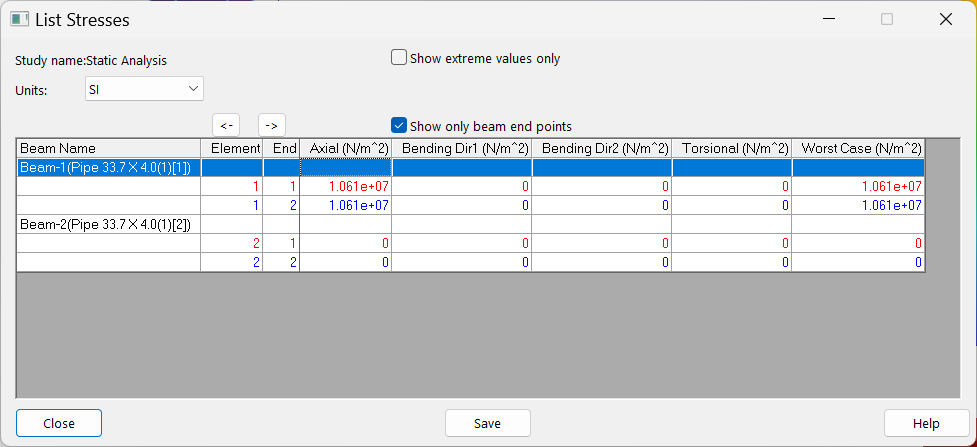
Das Fenster “Kräfte auflisten” ermöglicht es, durch die Werte der Axialkräfte zu navigieren, die in den verschiedenen Stäben der Struktur auftreten. Zum Beispiel ist $Beam-8$ das Element, das dem Stab $IH$ entspricht, der eine innere Axialkraft von ungefähr $688,7 kN$ erfährt (Abbildung 16).
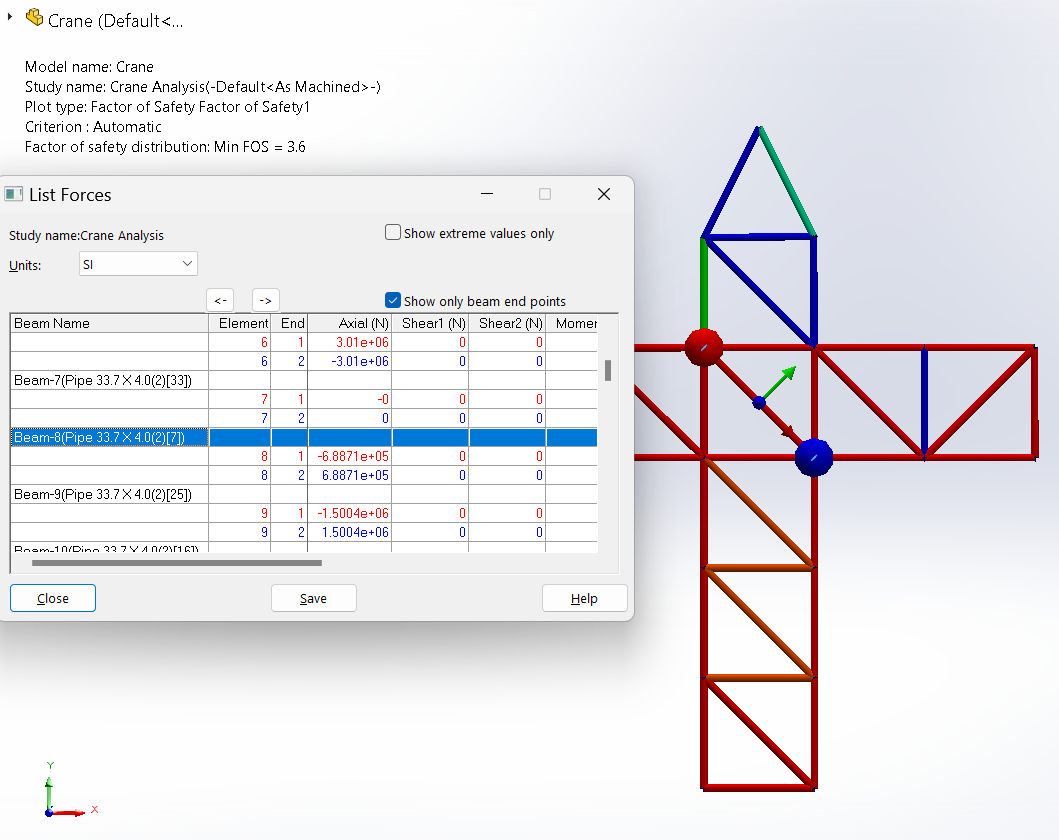
Dieser Wert ist etwa $3\%$ niedriger als der Wert der manuellen Berechnung $(707 \ kN)$ (Zugkraft), der in den folgenden Schritten ermittelt wird:
Einen Schnitt durch $KI$, $IJ$, $JH$ und $HT$ machen, wie in Abbildung 17(a) gezeigt.
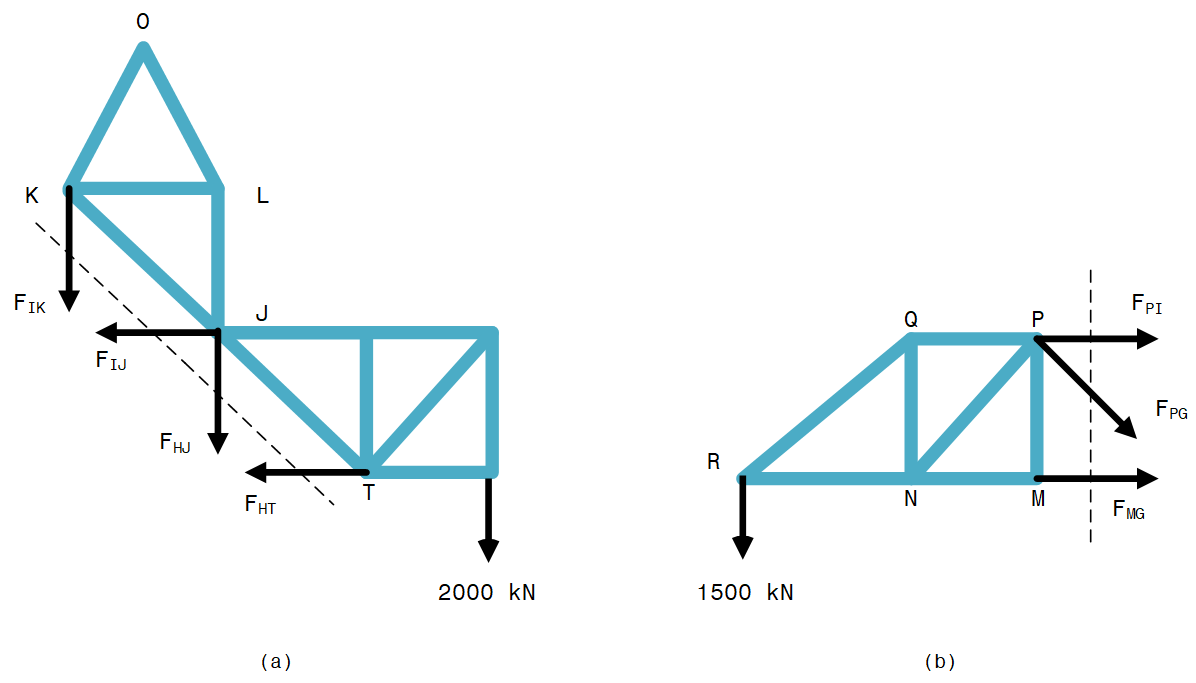
Momente um $J$ nehmen:
\[F_{HT} \times 3 + 2000 \times 6 = 0 \\ \Rightarrow F_{HT} = -4000 \ kN\]Horizontal auflösen:
\[F_{IJ} + F_{HT} = 0 \\ \Rightarrow F_{IJ} = +4000 \ kN\]Mit einem Schnitt durch $PI$, $PG$ und $MG$, wie in Abbildung 17(b) gezeigt, und mit Momenten um $G$:
\[F_{PI} \times 3 - 1500 \times 9 = 0 \\ \Rightarrow F_{PI} = +4500 \ kN\]Horizontale Auflösung bei $I$ in der vollständigen Stabkonstruktion:
\[F_{IH} \times cos45° + F_{IJ} - F_{IP} = 0 \\ \Rightarrow F_{IH} = +707 \ kN\]Die geringe Differenz zwischen dem Wert aus SOLIDWORKS und der manuellen Berechnung kann auf mögliche Rundungsfehler zurückzuführen sein.
PROBLEM 2: Durchführung einer statischen Analyse für zwei belastete, gerade verbundene Segmente einer Maschine
Problembeschreibung
Abbildung 18 zeigt zwei gerade Segmente einer wie abgebildet beladenen Maschine. Die Segmente bestehen aus legiertem Stahl und haben ein Querschnittsprofil mit einem Außen- und Innendurchmesser von $40 \ mm$ bzw. $20 \ mm$. Die Segmente werden als zwei miteinander verbundene Stäbe behandelt.
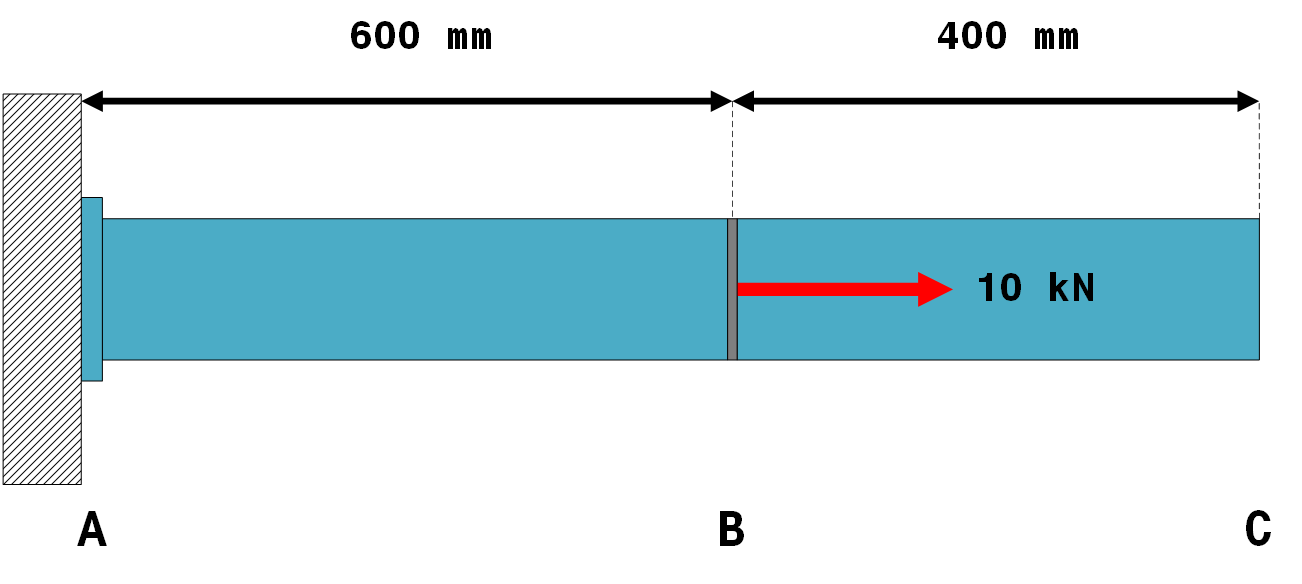
Ziele
Verwendung von SOLIDWORKS Simulation zur:
- Bestimmung der Verschiebung des Endes $C$.
- Bewertung der Axialspannungen, die sich bei der Belastung in den Bauteilen entwickeln.
Lösung
- Teil A - Erstellung des Skelettmodells des Balkens
- Teil B - Umwandlung des Skelettmodells in ein Strukturprofil
- Teil C - Erstellung der Simulationsstudie
- Teil D - Prüfung der Ergebnisse
Teil A - Erstellung des Skelettmodells des Balkens
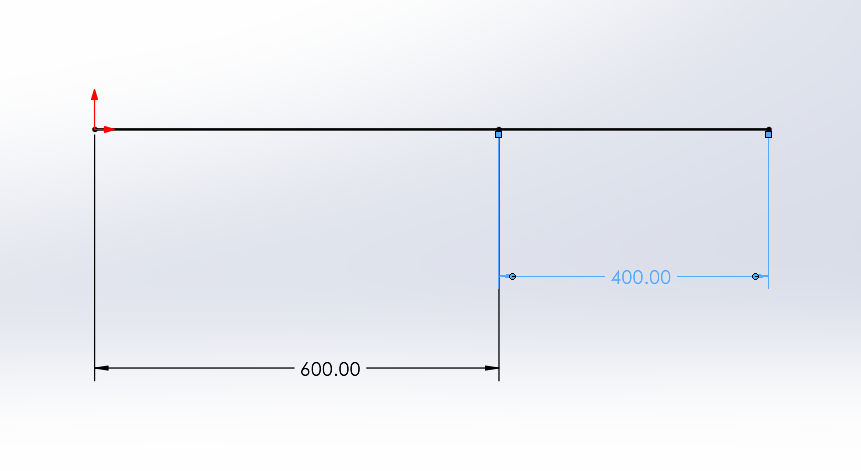
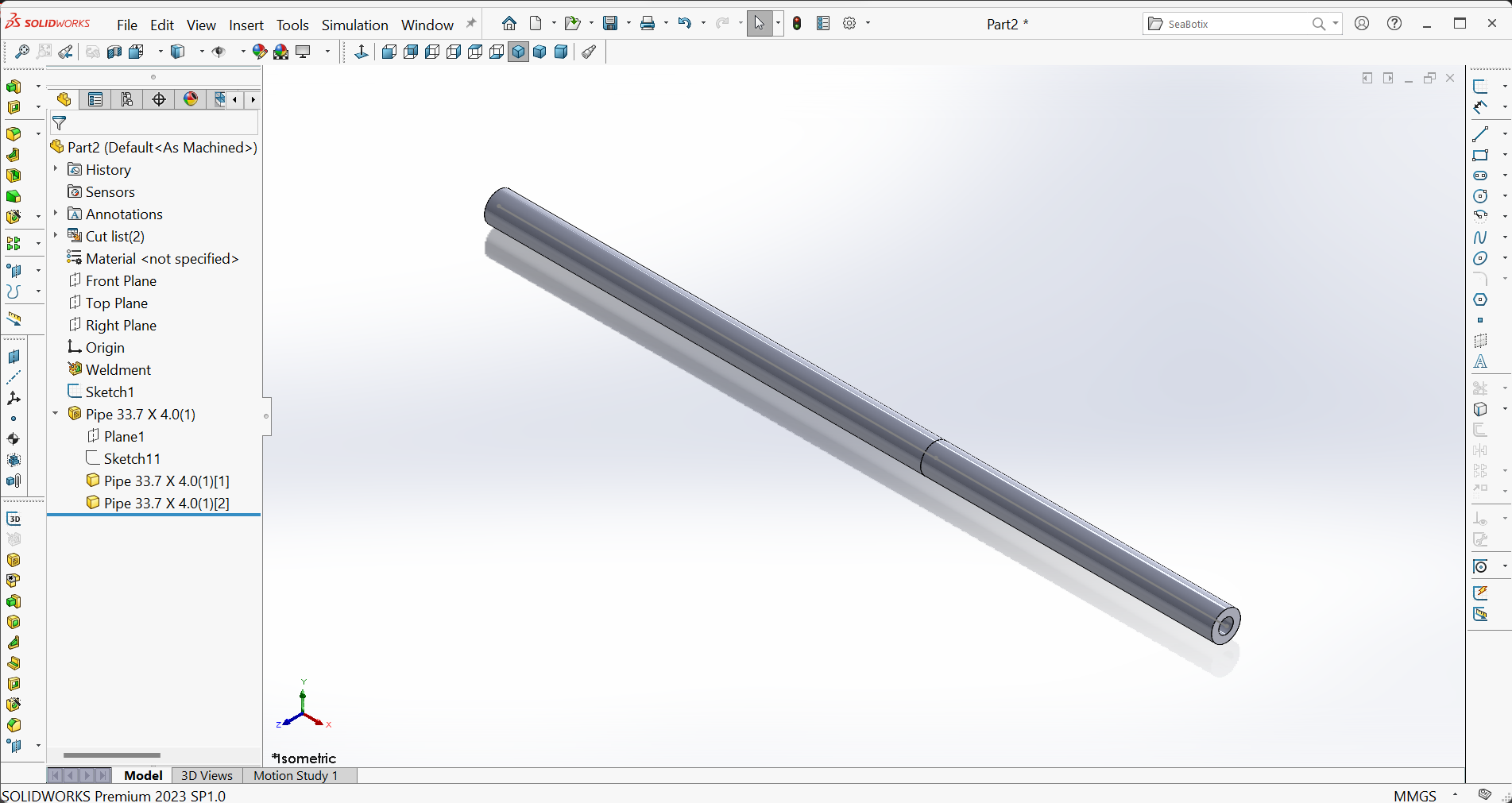
Teil B - Umwandlung des Skelettmodells in ein Strukturprofil
Abbildung 20 zeigt das Strukturmodell nach dem Hinzufügen von Struktureigenschaften zum Skelettmodell und der Bearbeitung des Querschnitts.
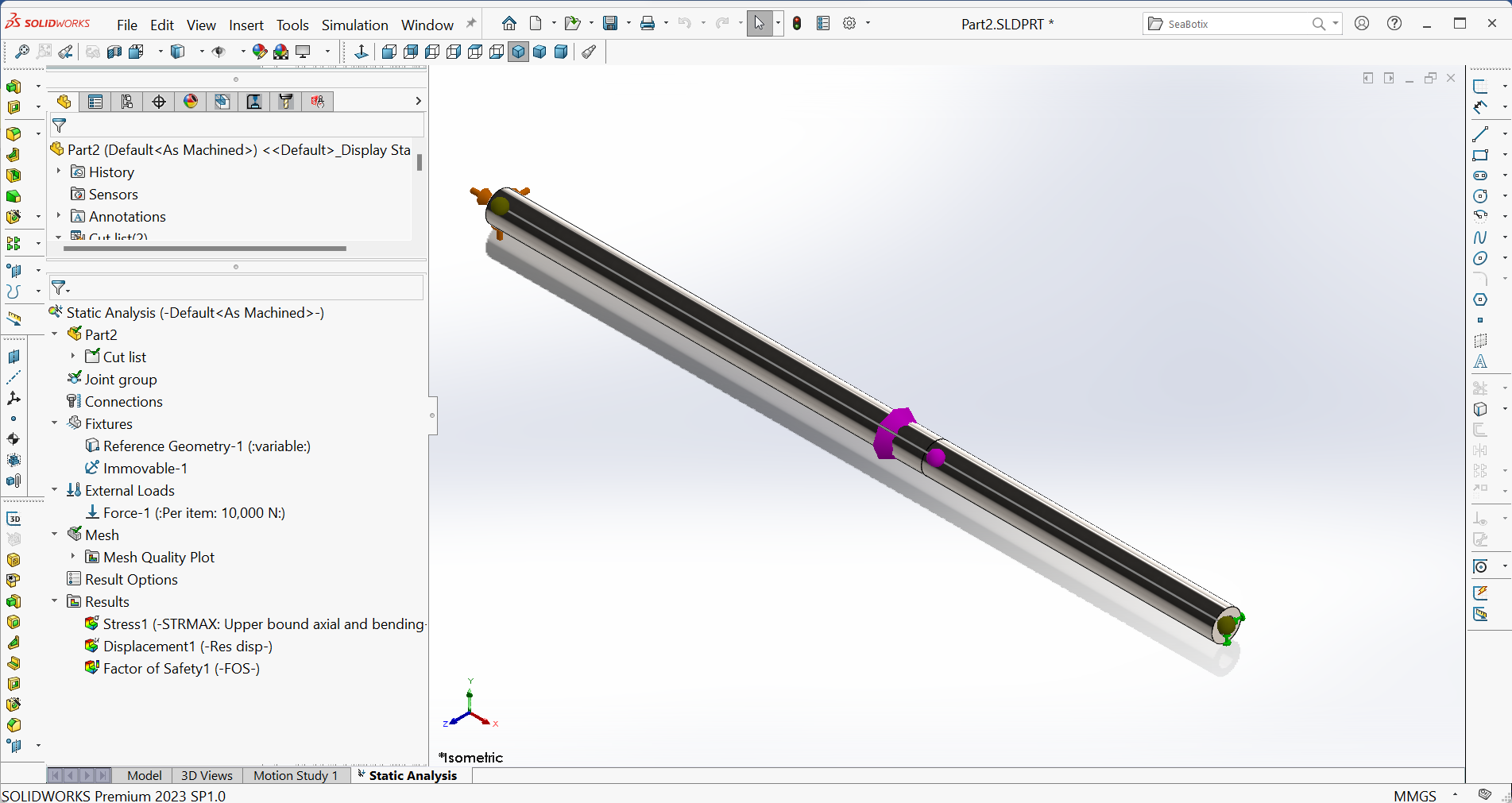
Teil C - Erstellung der Simulationsstudie
Abbildung 21 zeigt das Ergebnis der Erstellung einer neuen Studie, der Angabe des Materials für die Stäbe (legierter Stahl), des Wechsels von einem Balkenelement zu einem Stabelement, des Anbringens von Einspannungen (festes Auflager an der Verbindung $A$) und der Last sowie des Beginns des Vernetzungsvorgangs.
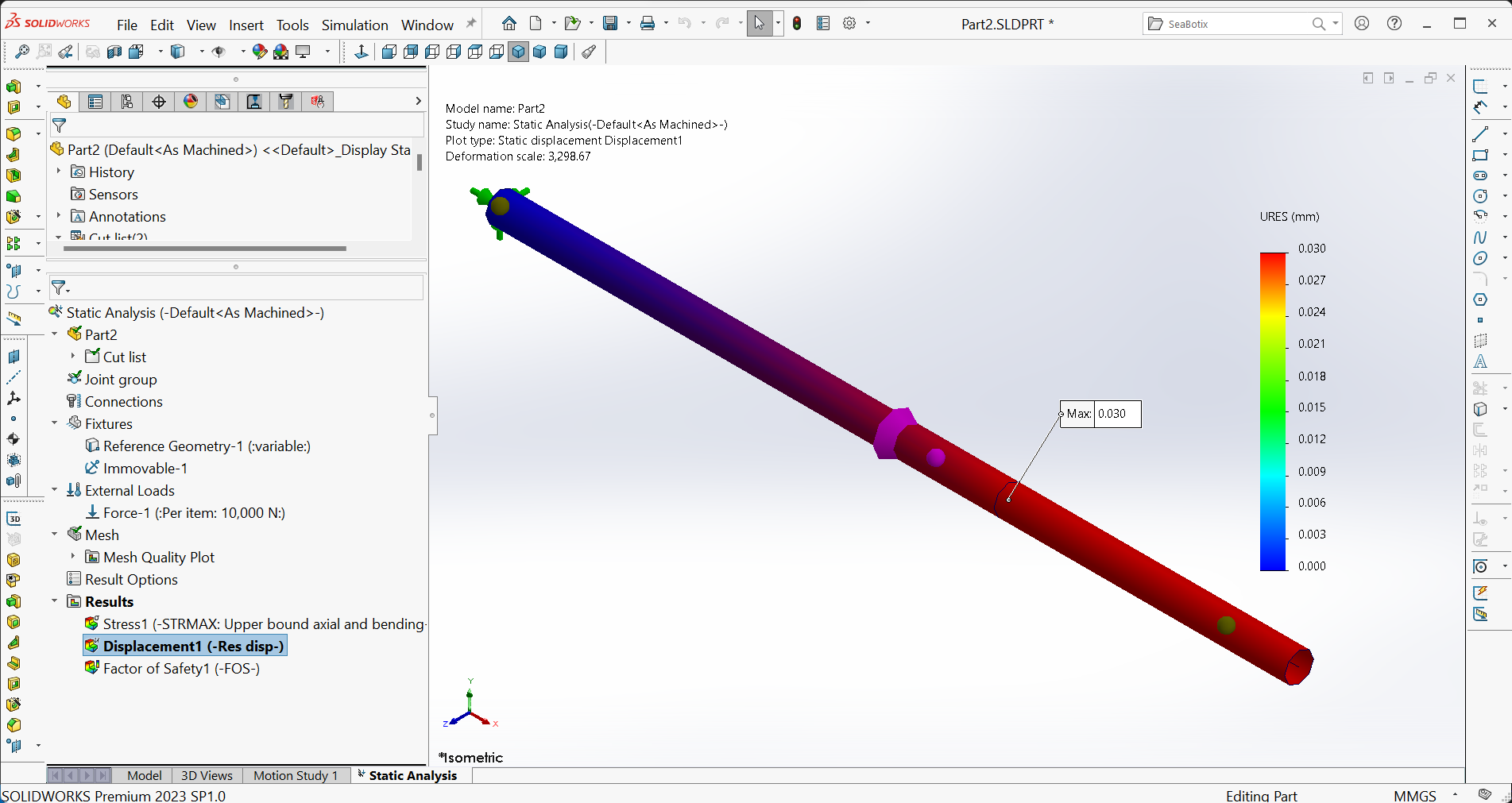
Teil D - Prüfung der Ergebnisse
- Maximale Verschiebung des Endes $C$: Abbildung 22 zeigt das Verschiebungsdiagramm und die maximale resultierende Verschiebung, die am Gelenk $B$ $(30 \ \mu m)$ auftritt und gleich der Verschiebung am Ende $C$ ist.
- Abrufen der Axialspannungen: Abbildung 23 zeigt die Standardanzeige der Axialspannungen.
PROBLEM 3: Durchführung einer statischen Analyse eines lasttragenden Mechanismus
Problembeschreibung
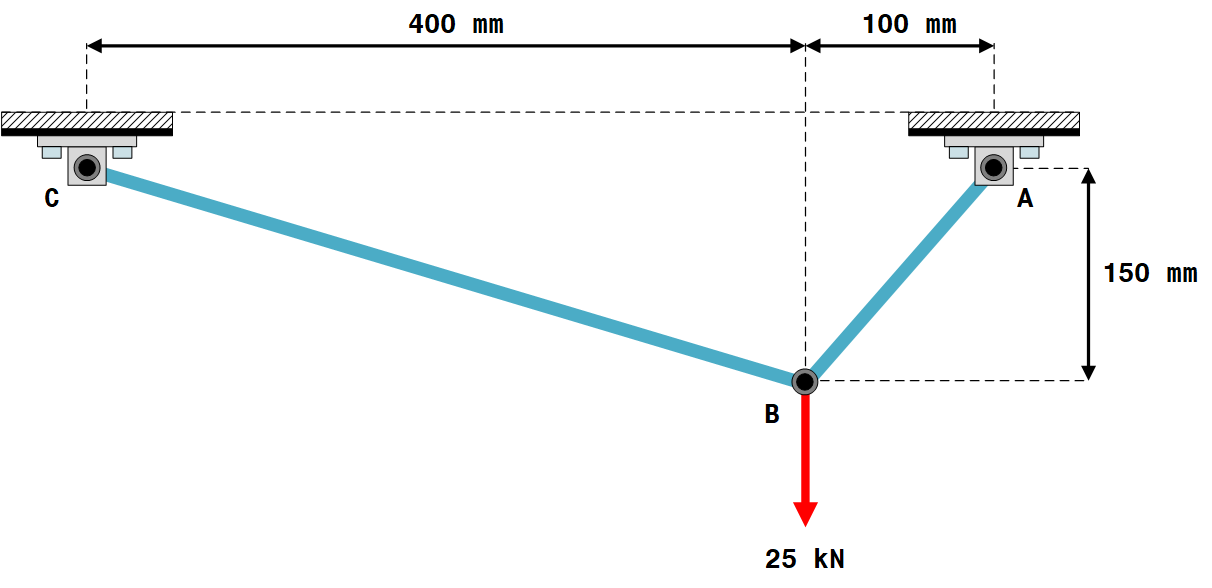
Abbildung 24 zeigt ein ebenes 2D-Fachwerk, das einen lasttragenden Mechanismus darstellt. Die Bauteile $CB$ und $AB$ bestehen aus $ASTM \ A-36$ Stahlrohren mit gleichem Querschnitt (Außen- und Innendurchmesser von $50 \ mm$ bzw. $30 \ mm$).
Ziele
Verwendung von SOLIDWORKS Simulation zum :
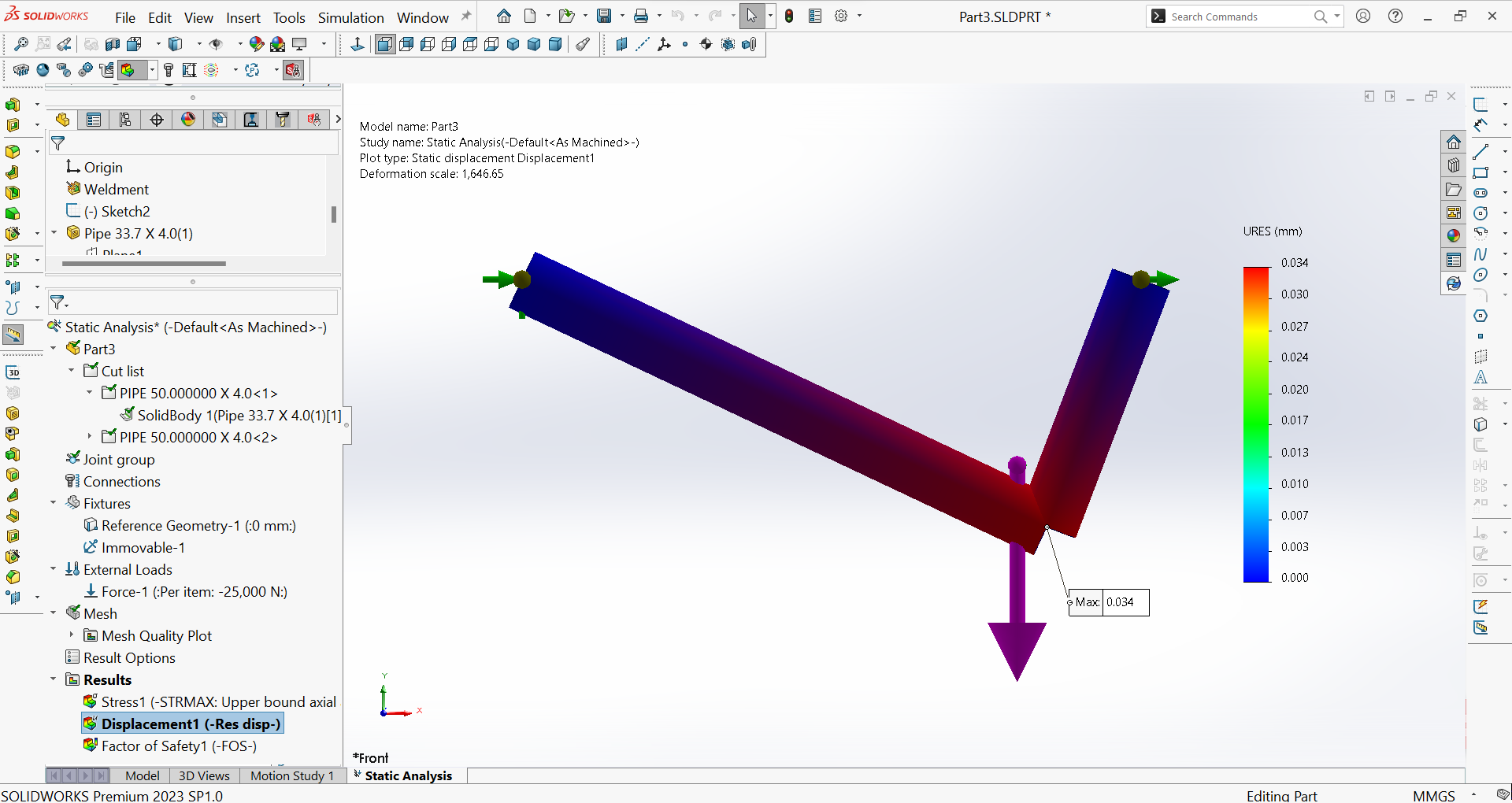
- Bestimmung der resultierenden Verschiebung der Verbindung $B$
- Bestimmung des Mindestsicherheitsfaktors der Baugruppe
Lösung
- Teil A - Erstellung des Skelettmodells des lasttragenden Mechanismus
- Teil B - Umwandlung des Skelettmodells in ein Strukturprofil
- Teil C - Erstellung der Simulationsstudie
- Teil D - Prüfung der Ergebnisse
Teil A - Erstellung des Skelettmodells des lasttragenden Mechanismus
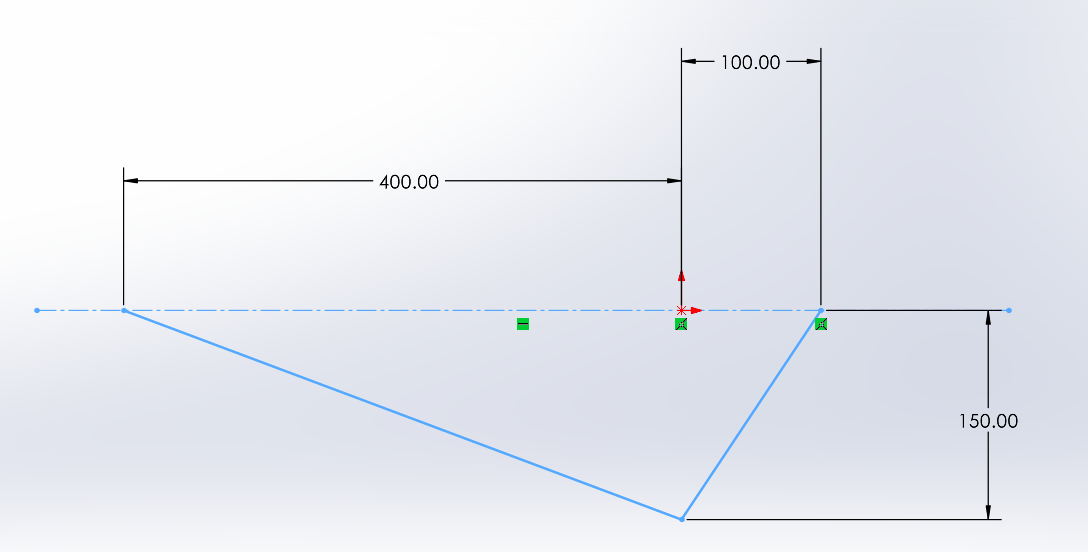
Teil B - Umwandlung des Skelettmodells in ein Strukturprofil
Abbildung 26 zeigt das Strukturmodell nach dem Hinzufügen von Struktureigenschaften zum Skelettmodell und der Bearbeitung des Querschnitts.
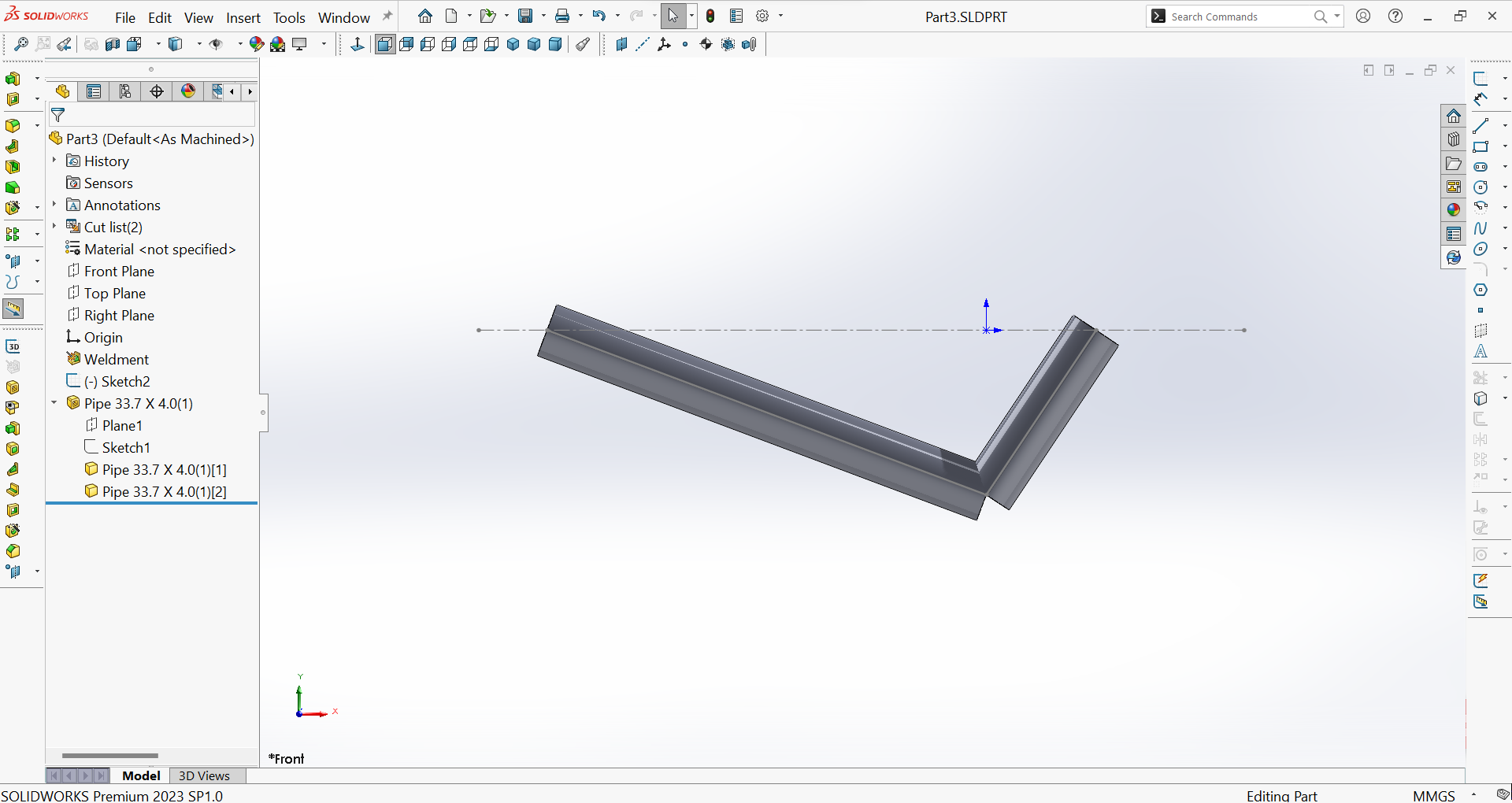
Teil C - Erstellung der Simulationsstudie
Abbildung 27 zeigt das Ergebnis der Erstellung einer neuen Studie, der Angabe des Materials für die Stäbe $(ASTM A-36 Stahl)$, des Wechsels von einem Balkenelement zu einem Stabelement, des Anbringens von Einspannungen (feste Auflager an den Verbindungsstellen $A$ und $C$) und der Belastung sowie des Beginns des Vernetzungsvorgangs.
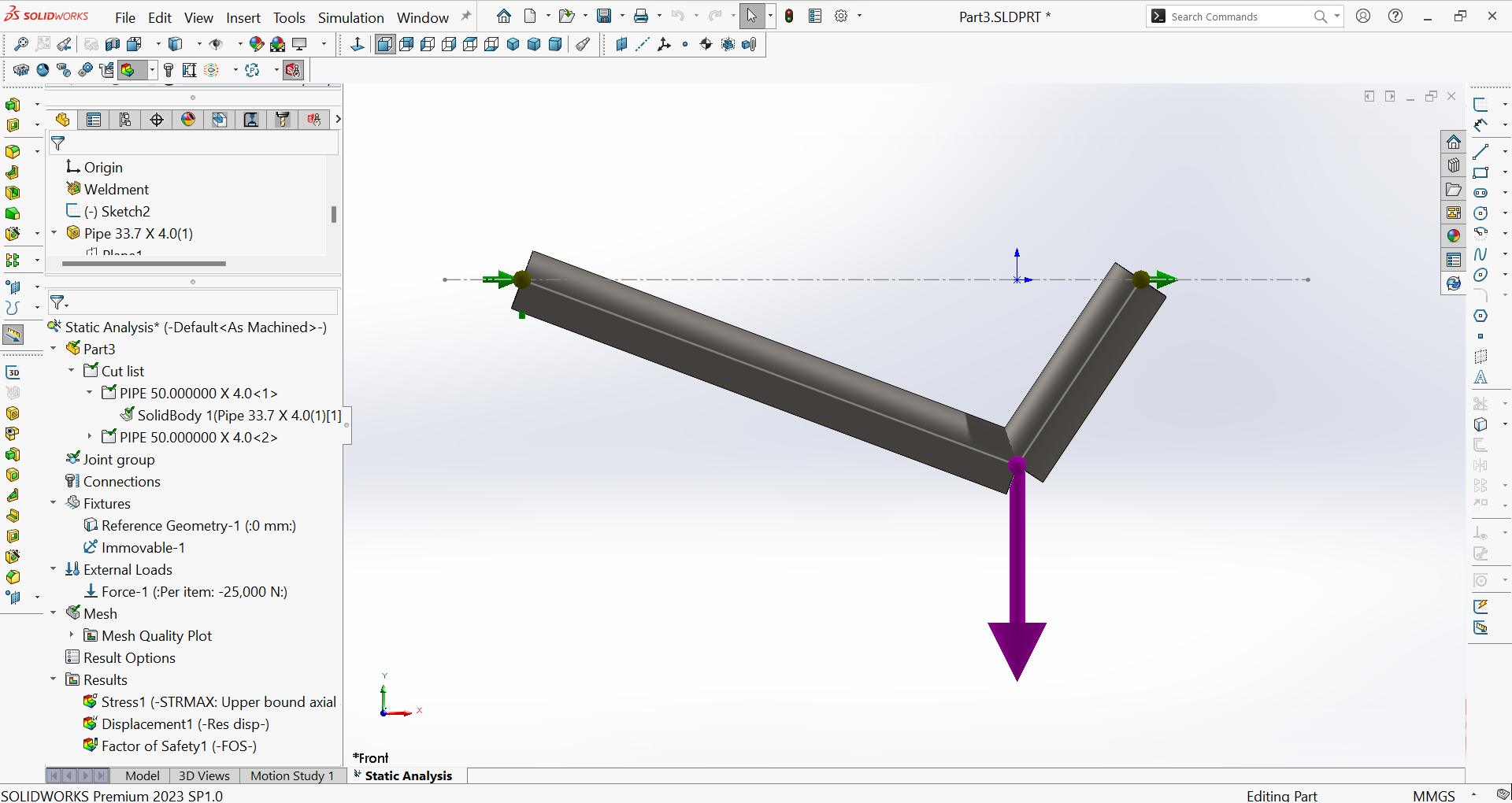
Teil D - Prüfung der Ergebnisse
- Resultierende Verschiebung des Gelenks $B$: Abbildung 28 zeigt das Verschiebungsdiagramm und die maximale resultierende Verschiebung, die an der Verbindung $B$ $(34 \ \mu m)$ auftritt.
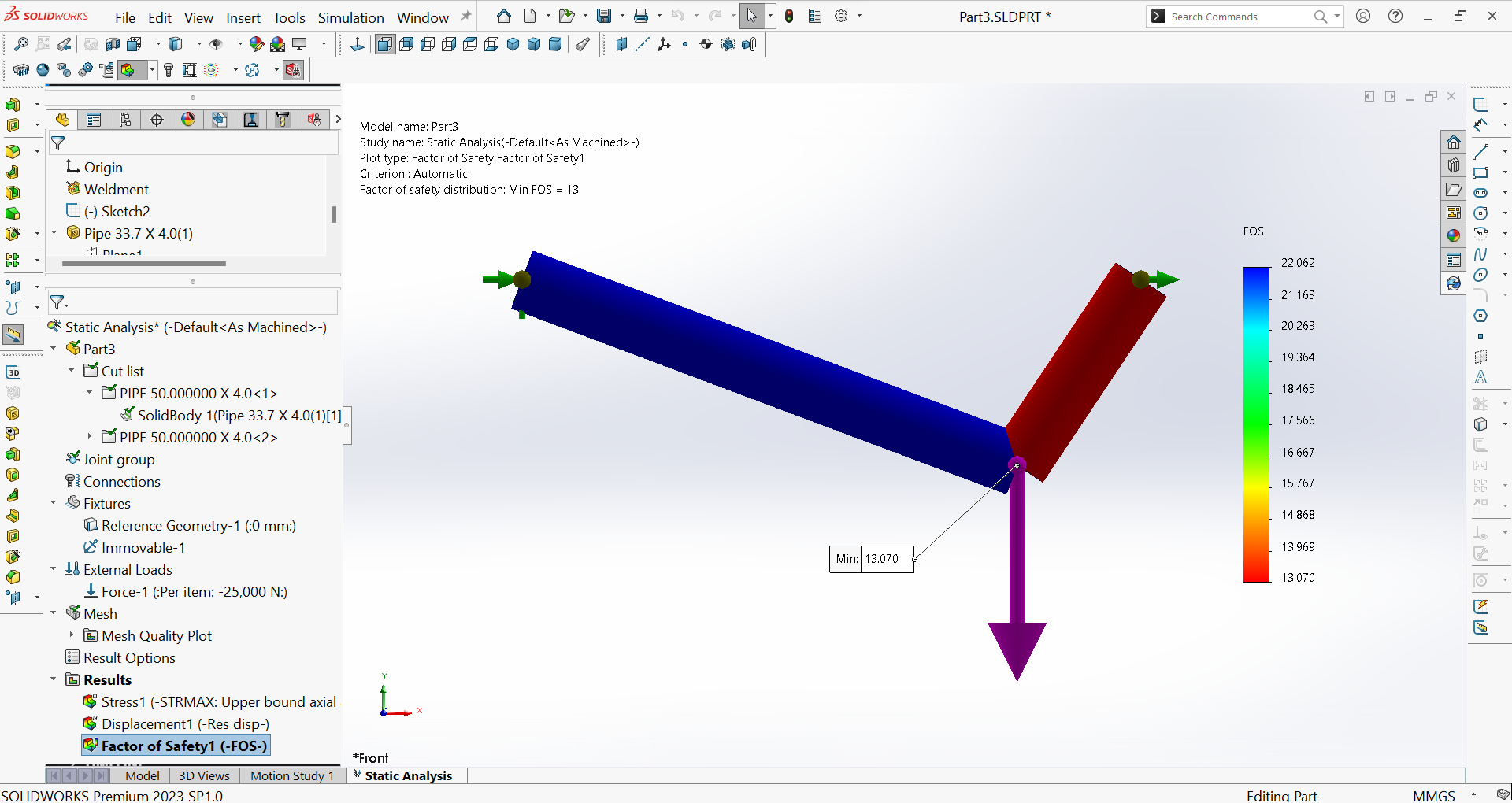
- Minimaler Sicherheitsfaktor der Baugruppe: Abbildung 29 zeigt den minimalen Sicherheitsfaktor der Baugruppe $(Min FOS = 13,07)$, was darauf hindeutet, dass das gewählte Material der Bauteile sicher ist.