Analytische und numerische Analyse und Lösung
von Spannungs- und Durchbiegungsaufgaben mithilfe von MATLAB
AUFGABE 1: Axiale Spannungen und Verformungen
Problembeschreibung
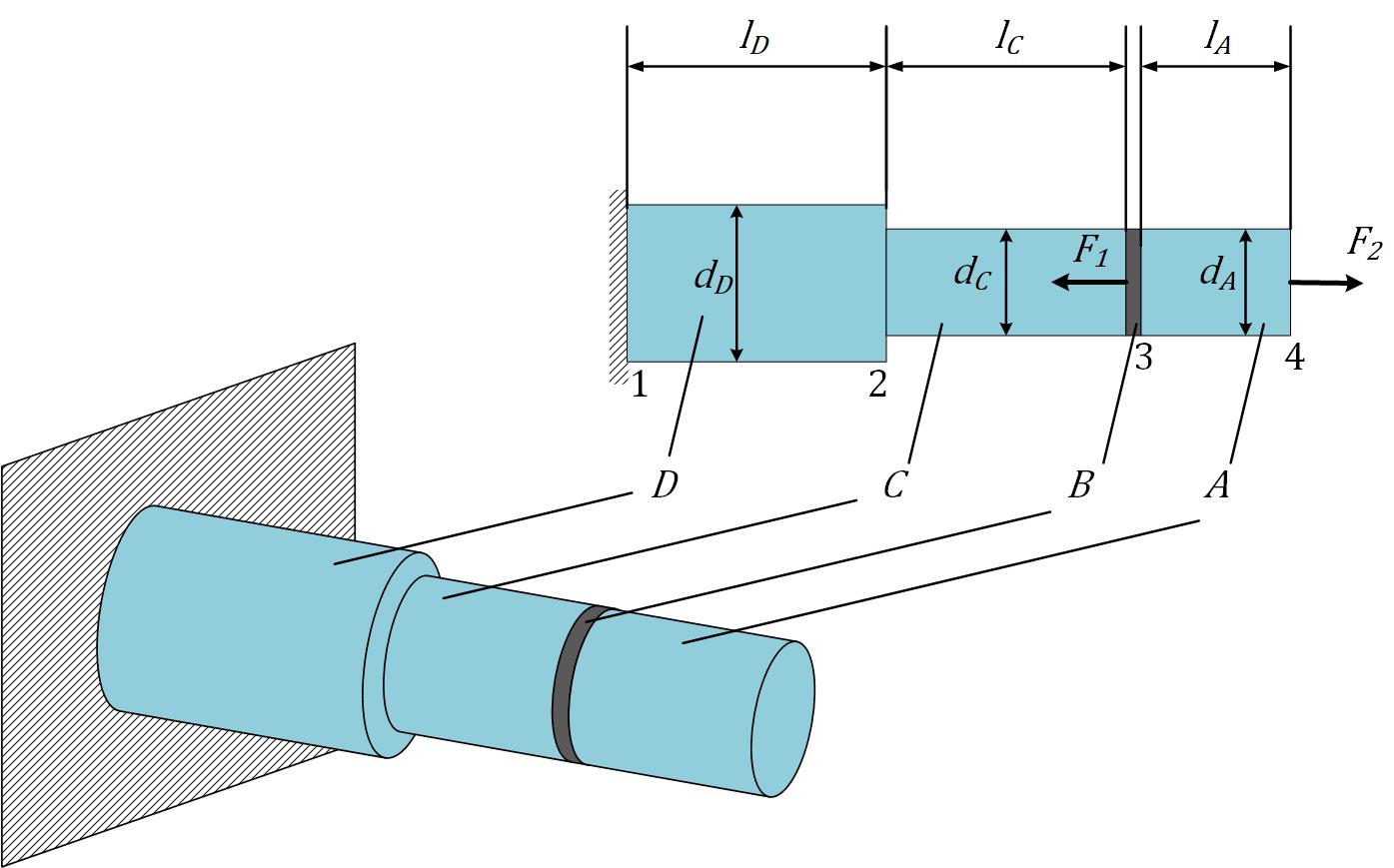
Eine starre Platte $\mathit{B}$ ist an den beiden Stäben $\mathit{A}$ und $\mathit{C}$ befestigt, wie in Abbildung 1 dargestellt. Der Stab $\mathit{C}$ ist an dem Stab $\mathit{D}$ befestigt, dessen Ende an einem starren Träger befestigt ist. Das Ende des Stabes $\mathit{A}$ ist frei. $l_{A}$, $l_{C}$, $l_{D}$ sind die Längen der Stäbe $\mathit{A}$, $\mathit{C}$ bzw. $\mathit{D}$, und ihre Durchmesser sind $d_{A}=d$, $d_{C}=d$ und $d_{D}=1,5d$. Die Last $F_{1}$ wird auf die starre Platte $\mathit{B}$ $($gleichmäßig um den Umfang der starren Platte $\mathit{B})$ verteilt, und die Last $F_{2}$ wird im Schwerpunkt des Endquerschnitts des Stabs $\mathit{B}$ aufgebracht.
Projektziele
Bestimmung der Axialspannungen in den Stäben $\mathit{A}$, $\mathit{C}$ und $\mathit{D}$, Verformungen der Stäbe und Gesamtverformung des Systems.
Für die numerische Anwendung könnten die folgenden Werte verwendet werden:
- $F_{1} = 64000 \hspace{1pt} N$
- $F_{2} = 192000 \hspace{1pt} N$
- $d = 45 \hspace{1pt} mm$
- $l_{A} = 170 \hspace{1pt} mm$
- $l_{C} = 144.5 \hspace{1pt} mm$
- $l_{D} = 255 \hspace{1pt} mm$
- Elastizitätsmodul $E = 21\cdot10^4 \hspace{1pt} MPa$
Lösung
Analytische Lösung
Der Stab wird in Komponenten unterteilt, und die Schnittgrößen werden berechnet, indem Abschnitte durch jede Komponente geführt werden. Für Teile des Stabs werden Freikörperdiagramme erstellt, wie in Abbildung 2A dargestellt.
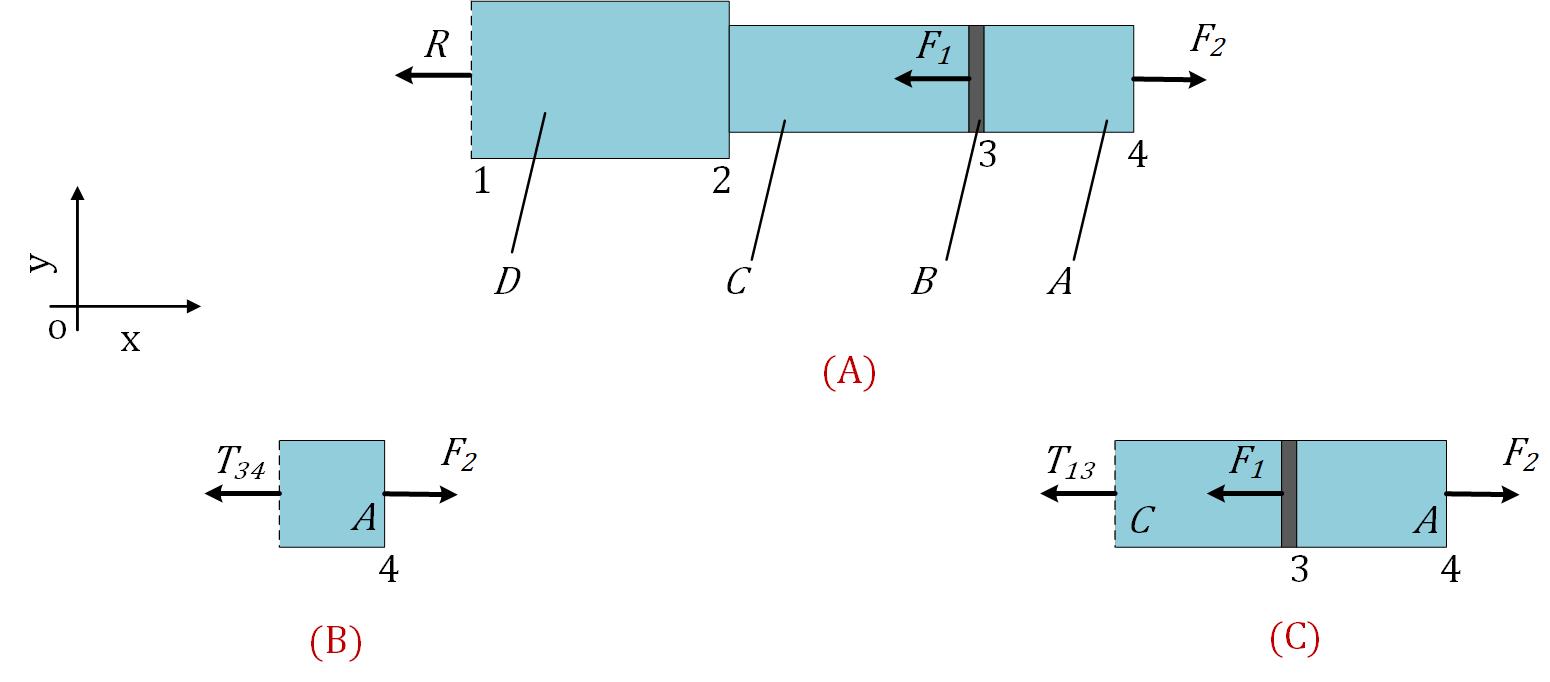
Das Freikörperdiagramm des Systems, nämlich Stab $\mathit{D}$, Stab $\mathit{C}$, Platte $\mathit{B}$ und Stab $\mathit{A}$, enthält nur eine unbekannte Kraft, nämlich die Reaktionskraft $\mathit{R}$ an der starren Auflage. Aus der Gleichgewichtsgleichung des Systems ergibt sich die Reaktionskraft $\mathit{R}$, also die Reaktionskraft der starren Lagerung auf den Stab D:
- $\sum_{}^{}\mathrm{F}_{x}^{A,B,C,D}=0$
- $\Leftrightarrow R+F_{1}-F_{2}=0$
- $\Leftrightarrow R = F_{2}-F_{1}$
Das MATLAB-Programm beginnt mit der Deklaration von Variablen als symbolische skalare Variablen mit Hilfe der syms-Funktion:
Dann werden die Schnittgrößen für jeden Teil des Stabes berechnet. Die Gleichgewichtsgleichung des Freikörperdiagramms für den Stab $A$, im Intervall $3-4$, Abbildung 2B, ergibt die Schnittkraft $T_{34}$:
- $\sum_{}^{}\mathrm{F}_{x}^{}=0$
- $\Leftrightarrow T_{34}-F_{2}=0$
- $\Leftrightarrow T_{34}=F_{2}$
Für den Bereich 1-3, Abbildung 2C, ergibt die Gleichgewichtsgleichung des Freikörperdiagramms die innere Kraft $T_{13}$:
- $\sum_{}^{}\mathrm{F}_{x}^{}=0$
- $\Leftrightarrow T_{13}+F_{1}-F_{2}=0$
- $\Leftrightarrow T_{13}=F_{2}-F_{1}$
Die oben ermittelten Gleichgewichtsgleichungen werden in MATLAB wie folgt geschrieben:
Die Querschnittsflächen der einzelnen Stäbe $A$, $C$ und $D$ werden wie folgt berechnet:
- $A_{A}=\frac{\pi d_{A}^{2}}{4}$
- $A_{C}=\frac{\pi d_{C}^{2}}{4}$
- $A_{D}=\frac{\pi d_{D}^{2}}{4}$
In MATLAB werden die Querschnittsflächen berechnet und die Ergebnisse ausgedruckt:
Die Axialspannungen an den Stäben $A$, $C$, $D$, nämlich $\sigma_{A}$, $\sigma_{C}$ und $\sigma_{D}$, werden berechnet unter Verwendung:
- $\sigma_{A}=\sigma_{34}=\frac{T_{34}}{A_{A}}=\frac{F_{2}}{A_{A}}=\frac{4F_{2}}{\pi d_{A}^{2}}$
- $\sigma_{C}=\sigma_{23}=\frac{T_{13}}{A_{C}}=\frac{F_{2}-F_{1}}{A_{C}}=\frac{4(F_{2}-F_{1})}{\pi d_{C}^{2}}$
- $\sigma_{D}=\sigma_{12}=\frac{T_{13}}{A_{D}}=\frac{F_{2}-F_{1}}{A_{D}}=\frac{4(F_{2}-F_{1})}{\pi d_{D}^{2}}$
In MATLAB werden die Axialspannungen berechnet durch:
Unter Berücksichtigung der folgenden Punkte:
- Hookesches Gesetz der Elastizität: $\sigma=E\epsilon$, d. h. für kleine Verformungen ist die Spannung direkt proportional zur Dehnung (die sie hervorgerufen hat),
- und der Ausdruck für die elastische Dehnung: $\epsilon=\frac{\delta}{l}$, wobei $l$ die Länge des Stabes, $\epsilon$ das griechische Symbol für die Dehnung (dimensionslos) und $\delta$ die Gesamtdehnung (oder die Dehnung des Stabes) ist,
werden die axialen Verschiebungen (d. h. die Dehnung, die sich bei Zugbelastung eines geraden Stabes ergibt) der Stäbe $C$, $D$ und des Systems berechnet:
- Axiale Verschiebung des Stabes $D$: $$ \delta_{12}=\frac{T_{13}l_{D}}{A_{D}E}=\frac{(F_{2}-F_{1})l_{D}}{A_{D}E} $$
- Axiale Verschiebung des Stabes $C$: $$ \delta_{23}=\frac{T_{13}l_{C}}{A_{C}E}=\frac{(F_{2}-F_{1})l_{C}}{A_{C}E} $$
- Axiale Verschiebung der Stäbe $D$ und $C$: $$ \delta_{13}=\delta_{12}+\delta_{23}=\frac{T_{13}l_{D}}{A_{D}E} $$ $$ =\frac{(F_{2}-F_{1})l_{D}}{A_{D}E}+\frac{(F_{2}-F_{1})l_{C}}{A_{C}E} $$ $$ =\frac{(F_{2}-F_{1})}{E}\left( \frac{l_{D}}{A_{D}}+\frac{l_{C}}{A_{C}} \right) $$
- Axiale Verschiebung des Stabes $A$: $$ \delta_{34}=\frac{T_{34}l_{A}}{A_{A}E}=\frac{F_{2}l_{A}}{A_{A}E} $$
- Gesamte axiale Verschiebung des Systems: $$ \delta_{14}=\delta_{13}+\delta_{34} $$ $$ =\frac{(F_{2}-F_{1})}{E}\left( \frac{l_{D}}{A_{D}}+\frac{l_{C}}{A_{C}} \right) +\frac{F_{2}l_{A}}{A_{A}E} $$
In MATLAB wird die axiale Verschiebung der Stäbe und des Systems berechnet:
Numerische Lösung
Zur numerischen Berechnung der Axialspannungen und -verschiebungen werden zunächst die in der Aufgabenstellung angegebenen numerischen Daten in den MATLAB-Code eingegeben und dann die symbolischen Variablen durch die numerischen Daten ersetzt. Für den ersten Teil werden zwei Zell-Arrays eingeführt. Die String-Werte (die symbolischen Variablen) der numerischen Daten werden in Cell Array lists und ihre numerischen Werte in Cell Array listn eingetragen. Im zweiten Teil wird die symbolische Substitutionsfunktion subs von MATLAB verwendet, um die symbolischen Variablen in lists durch die entsprechenden Werte aus listn zu ersetzen, die dann auf dem Bildschirm angezeigt werden.
In ähnlicher Weise werden die numerischen Werte jedes Stabdurchmessers angezeigt und die Querschnittswerte mit Hilfe der MATLAB-Funktion eval berechnet und angezeigt:
Die numerischen Werte der einzelnen Stäbe werden in MATLAB durch ausgedrückt:
Schließlich werden die numerischen Werte der Axialspannungen berechnet und in MATLAB dargestellt:
und die Ergebnisse sind:
Die numerischen Werte für die axiale Verschiebung der Stäbe und des Systems werden in MATLAB berechnet:
und die Ergebnisse sind:
Diagramme
Die Kraft-, Spannungs- und Verschiebungsdiagramme (Abbildung 3) werden mithilfe des folgenden MATLAB-Codes erstellt:
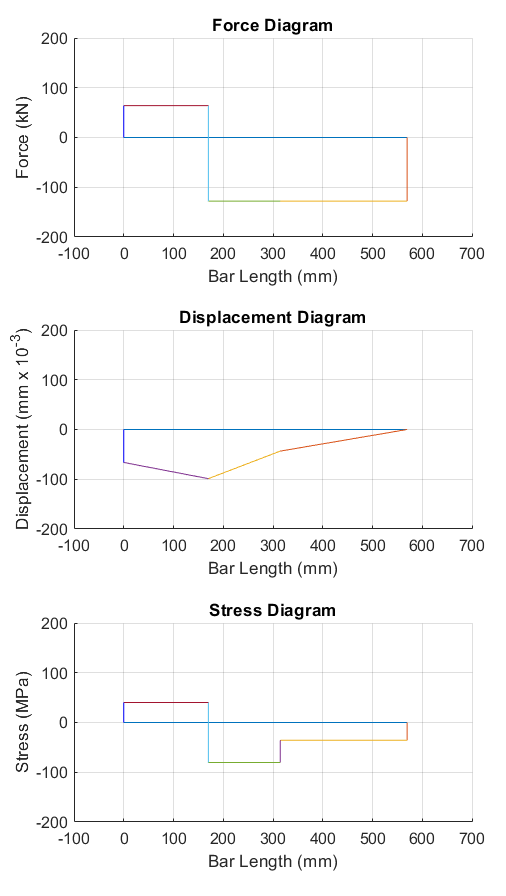
Zur Erstellung der Diagramme werden drei MATLAB-Funktionen verwendet, und zwar: ForceDdraw, StressDdraw und DisplacementDdraw, unter Verwendung der line-Funktion, die zwei Eingangsargumente benötigt. Diese Funktion zeichnet Linien in den aktuellen Achsen, indem sie die Daten in beiden Eingangsvektoren (oder Matrizen) verbindet. In diesem Fall sind beide Eingangsargumente Vektoren, wobei der erste Vektor die $x$-Koordinaten und der zweite Vektor die $y$-Koordinaten sind. Da beide Eingangsvektoren gleich lang sind, zeichnet die line-Funktion bei jeder Anwendung eine einzige Linie. Die Codes für die drei MATLAB-Funktionen sind wie folgt:
- Die MATLAB-Funktion
ForceDdraw: - Die MATLAB-Funktion
StressDdraw: - Die MATLAB-Funktion
DisplacementDdraw:
AUFGABE 2: Biege- und Schubspannungen
Problembeschreibung
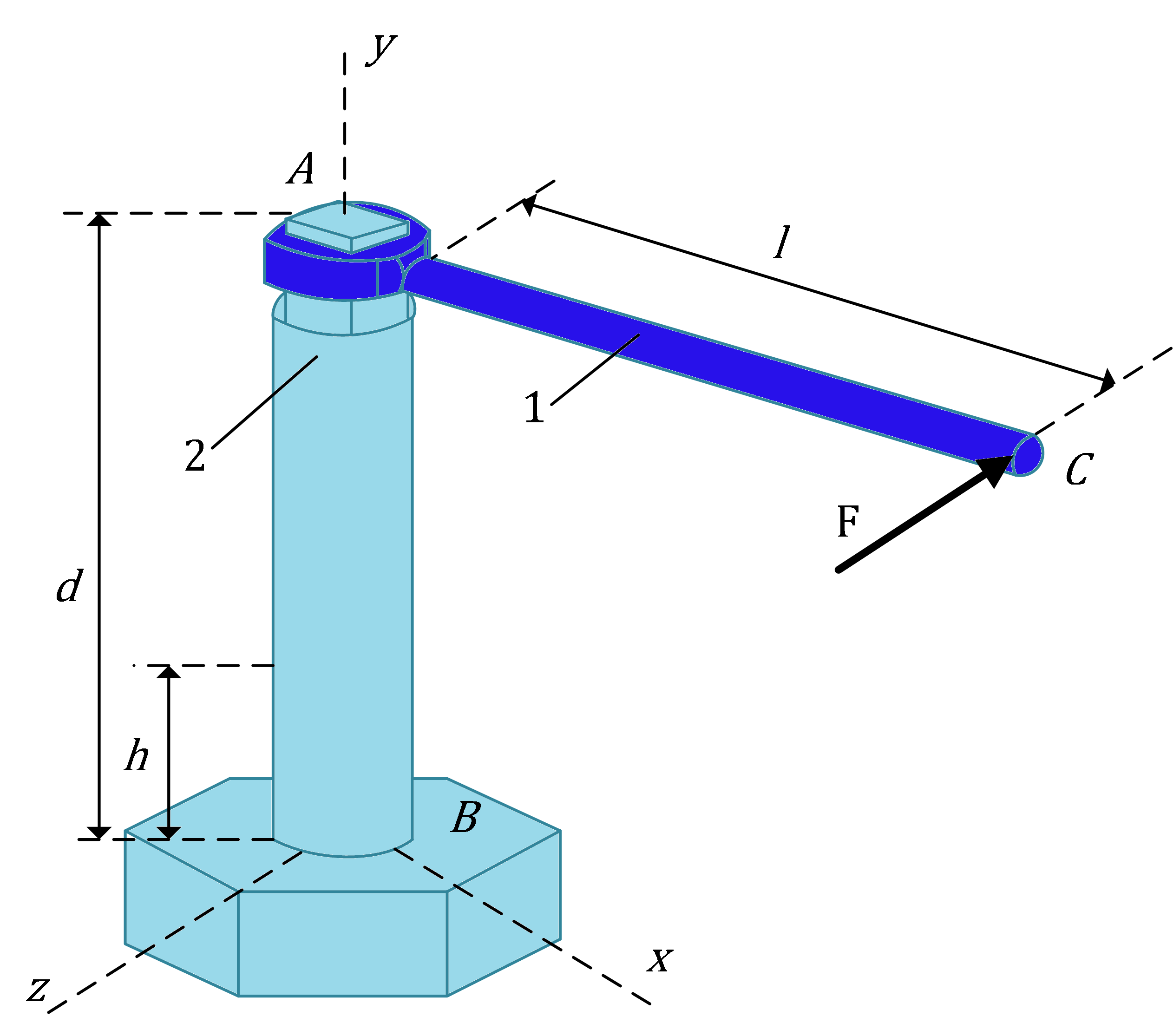
Ein Hebel $(1)$ der Länge $AC = l$ sitzt auf einem verjüngten Hebelstab $(2)$, bezeichnet mit $AB$. Der Hebel wird an seinem Ende mit einer horizontalen Kraft $F$ belastet, wie in Abbildung 4 dargestellt. Der Hebelstab hat den Radius $r$ und die Länge $d$.
Für die numerische Berechnung können die folgenden Werte verwendet werden:
- $F = 250 \hspace{1pt} N$
- $d = 200 \hspace{1pt} mm$
- $l = 250 \hspace{1pt} mm$
- $h = 50 \hspace{1pt} mm$
- $r = 9 \hspace{1pt} mm$
Projektziele
- Bestimmung der Normal- und Schubspannungen eines Elements, das sich auf der freien Oberfläche des Hebelstabs $(2)$ im Abstand $h$ von der sechseckigen Basis befindet (das Element liegt parallel zu der durch die Achsen $x$, $y$ bestimmten Ebene).
- Konstruktion des Mohrschen Spannungskreises und Bestimmung der Hauptebenen und Spannungen.
Lösung
Die Kraft $F$ bewirkt ein Biegemoment (reine Biegung) und ein Drehmoment (Torsionsmoment) auf den Stab. Durch die Biegung werden also Biegespannungen, die Normalspannungen sind, und über den Querschnitt verteilte Schubspannungen erzeugt.
Die Normal- und Schubspannungen eines allgemeinen Elements parallel zur Ebene, die durch die Achsen $x$, $y$ im Abstand $h$ von der hexagonalen Basis bestimmt wird, sind $\sigma_{y}$ bzw. $\tau_{yz}$.
Biegespannungen
$\sigma_{y}$ ist die Biegespannungsverteilung über die Biegehöhe, für den Fall der reinen Biegung:
\[\sigma_{y}(z)=\frac{M_{b,x}}{I_{x}}\cdot z\]Die verschiedenen tiefgestellten Buchstaben drücken aus, dass die Biegespannung in $y$-Richtung über die hier durch die $z$-Koordinate definierte Biegehöhe verteilt wird, und $x$ ist die neutrale Achse.
- $M_{b,x}$ ist das Biegemoment, es entspricht:
- $I_{x}$ ist das Flächenträgheitsmoment. Es ist eine geometrische Eigenschaft einer Form, die die Verteilung von Punkten um eine Achse beschreibt. In der klassischen Mechanik wird es als Maß für den Widerstand eines Körpers gegen Biegung verwendet. Für einen kreisförmigen Querschnitt ist es gleich:
- Die Biegehöhe $z$ ist der senkrechte Abstand eines Punktes entlang des Querschnittes des Stabes von seiner neutralen Achse, und bei der Berechnung der maximalen Biegespannung ist $z$ gleich $r$, weil dort die Biegespannung entlang des Querschnittes ihren Höchstwert erreicht.
Die Gleichung für die Biegespannung zeigt, dass die Biegespannung linear zunimmt, wenn das Biegemoment und der Abstand von der neutralen Achse zunehmen, und dass sie abnimmt, wenn das Flächenträgheitsmoment zunimmt. Die maximale Spannung tritt an den am weitesten von der neutralen Achse entfernten Fasern auf. Der Term $\frac{z}{I_{x}}$ hängt nur von der Geometrie des Querschnitts ab.
Die maximale Biegespannung ist somit gleich:
\[\sigma_{y}=\frac{M_{b,x}}{I_{x}}\cdot r\]Schubspannungen
Torsion ist die Verdrehung eines Objekts, die durch ein um die Längsachse des Objekts wirkendes Moment verursacht wird. Ein Moment, das die Tendenz hat, eine Verdrehung zu verursachen, wird als Drehmoment bezeichnet.
Die Torsion erzeugt Schubspannungen und -verformungen innerhalb des Stabes. Sowohl die Schubspannungen als auch die Schubverformungen nehmen linear mit dem Abstand von der Mitte des Querschnitts zu, wobei die maximale Schubspannung und Schubverformung an der Außenfläche auftritt.
Die maximale Schubspannung aufgrund von Torsion für einen kreisförmigen Querschnitt ist gegeben durch die Gleichung:
\[\tau = \frac{T_{y}\cdot r}{J_{p}}\]Das heißt, die Schubspannung ist eine Funktion von
- dem Drehmoment $T_{y}$, hier: um die $y$-Achse,
- dem Abstand von der Mitte des Querschnitts, hier: gleich $r$; dem Abstand zum Rand,
- und dem polaren Trägheitsmoment $J_{p}$.
Für einen kreisförmigen Querschnitt beträgt das polare Trägheitsmoment:
\[J_{p} = \frac{\pi \cdot r^{4}}{2}\]Das Drehmoment $T_{y}= F \cdot l$.
\[\Rightarrow \tau = \frac{2F \cdot l}{\pi \cdot r^{3}}\]** Spannungstransformation und Mohrscher Spannungskreis**
Betrachtet man ein 2D-Spannungselement, das einem ebenen Spannungszustand (z.B. der $xy$-Ebene) entspricht, so werden die vier Flächen des Elements durch Normal- und Schubspannungen beansprucht. Angenommen, dieses Element wird von einer schrägen Ebene mit einer Normalen in einem beliebigen Winkel $\phi$ gegen den Uhrzeigersinn von der $x$-Achse geschnitten, dann könnten die Werte der Normal- und Schubspannungen mit Hilfe der Spannungstransformationsgleichungen berechnet werden:
- $\sigma = \frac{\sigma_{x}+\sigma_{y}}{2}+\frac{\sigma_{x}-\sigma_{y}}{2}\cdot cos(2\phi)+\tau_{xy}\cdot sin(2\phi)$
- $\tau = \frac{\sigma_{x}-\sigma_{y}}{2}\cdot sin(2\phi)+\tau_{xy}\cdot cos(2\phi)$
Durch Differenzieren der ersten Gleichung nach $\phi$ und Gleichsetzen des Ergebnisses mit Null wird $\sigma$ maximiert und ergibt sich:
- $tan(2\phi)=\frac{2\tau_{xy}}{\sigma_{x}-\sigma_{y}}$
Diese Gleichung definiert zwei bestimmte Werte für den Winkel $2\phi$, von denen einer die maximale Normalspannung $\sigma_{1}$ und der andere die minimale Normalspannung $\sigma_{2}$ definiert. Diese beiden Spannungen werden als Hauptspannungen bezeichnet, und ihre entsprechenden Richtungen als Hauptrichtungen. Der Winkel zwischen den beiden Hauptrichtungen ist $90°$. Diese Gleichung lässt sich aus der zweiten Gleichung der Spannungstransformationsgleichungen ableiten, indem $\tau =0$ gesetzt wird, was bedeutet, dass die senkrechten Flächen mit den Hauptspannungen keine Schubspannungen aufweisen.
Wichtig ist, dass die Winkel im Mohrschen Spannungskreis im Vergleich zum Drehwinkel des Spannungselements verdoppelt werden. Bei Betrachtung des Mohrschen Spannungskreises ergibt sich zum Beispiel ein Winkel von $180$ Grad zwischen der minimalen und der maximalen Hauptspannung, während der Winkel beim Spannungselement $90$ Grad beträgt. Aus diesem Grund wird auf dem Mohrschen Spannungskreis die Notation $2\phi$ verwendet. $\phi$ ist der Drehwinkel des Spannungselements, und $2\phi$ ist der entsprechende Winkel auf dem Mohrschen Spannungskreis.
Die Formeln für die beiden Hauptspannungen lassen sich durch Einsetzen des Winkels $2\phi$ in die erste Spannungstransformationsgleichung ermitteln:
- $\sigma_{1}, \sigma_{2} =\frac{\sigma_{x}+\sigma_{y}}{2}\pm \sqrt{({\frac{\sigma_{x}-\sigma_{y}}{2})^{2}}+\tau_{xy}^{2}}$
In ähnlicher Weise erhält man durch Differenzieren der zweiten Spannungstransformationsgleichung nach $\phi$ und Gleichsetzen des Ergebnisses mit Null:
- $tan(2\phi)=-\frac{\sigma_{x}-\sigma_{y}}{2\tau_{xy}}$
Damit sind die beiden Werte von $2\phi$ definiert, bei denen die Schubspannung $\tau$ einen extremen Wert (nicht das Maximum) erreicht. Der Winkel zwischen den beiden Flächen mit den maximalen Schubspannungen beträgt $90°$.
Die Formeln für die beiden extremen Schubspannungen werden durch den Einsatz des Winkels $2\phi$ in der zweiten Spannungstransformationsgleichung ermittelt:
- $\tau_{1}, \tau_{2} =\pm \sqrt{({\frac{\sigma_{x}-\sigma_{y}}{2})^{2}}+\tau_{xy}^{2}}$
Analytische Lösung
Das MATLAB-Programm beginnt mit der Deklaration von Variablen als symbolische skalare Variablen mit Hilfe der syms-Funktion:
Anschließend werden die Normal- und Schubspannungen in MATLAB berechnet:
Dies führt zu der folgenden Ausgabe:
Anschließend werden die Elementorientierung und die Hauptspannungen in MATLAB berechnet:
Dazu wird die vom Benutzer erstellte Funktion mohr2D(sigma_x,sigma_y,tau,phi) benötigt, um zu berechnen:
- die maximale Normalspannung $\sigma_{1}$ (
sigma_max) und die minimale Normalspannung $\sigma_{2}$ (sigma_min). Der Mohrsche Spannungskreis kreuzt die horizontale Achse an diesen beiden Stellen, da die Schubspannung Null ist. Diese beiden Werte können auch berechnet werden, indem man die $x$-Koordinate des Kreismittelpunkts nimmt und den Kreisradius addiert oder subtrahiert - der Radius (
Radius) des Mohrschen Spannungskreises, der gleich $\sqrt{({\frac{\sigma_{x}-\sigma_{y}}{2})^{2}}+\tau_{xy}^{2}}$ ist, was auch der Wert der maximalen Schubspannung ist - der Mittelpunkt (
Zentralkreis) des Mohrschen Spannungskreises, der bei $(\frac{\sigma_{x}+\sigma_{y}}{2},0)$ liegt - der Winkel $\phi$, im Code
phigenannt, zwischen dem ursprünglichen Spannungselement und den Hauptebenen. $tan(2\phi)$ wird im Code alsphi_pbezeichnet.
Diese Funktion wird durch den folgenden Code erzeugt:
Und die Ausgabe dieses Codes ist:
Numerische Lösung
Für die numerischen Berechnungen werden die numerischen Daten für die aufgebrachte Kraft $F$, die Länge des Hebels $l$, den Radius $r$ und die Länge $d$ des Hebelstabs sowie den Abstand $h$ des Elements auf dem Hebelstab in MATLAB als Eingabe eingegeben:
Die numerischen Werte für das äquivalente Kräftesystem; Drehmoment $T_{y}$, Kraft $F$ und Biegemoment $M_{b,x}$, werden in MATLAB berechnet und ausgedruckt:
was zur Folge hatte:
Die numerischen Werte für die Spannungsausrichtung und die Hauptspannungen werden in MATLAB berechnet und angezeigt:
was zur Folge hatte:
Grafische Darstellung
Die grafische Darstellung des Mohrschen Spannungskreises (Abbildung 5) wird in MATLAB durch Aufruf der benutzerdefinierten Funktion mohr2Ddraw erstellt:
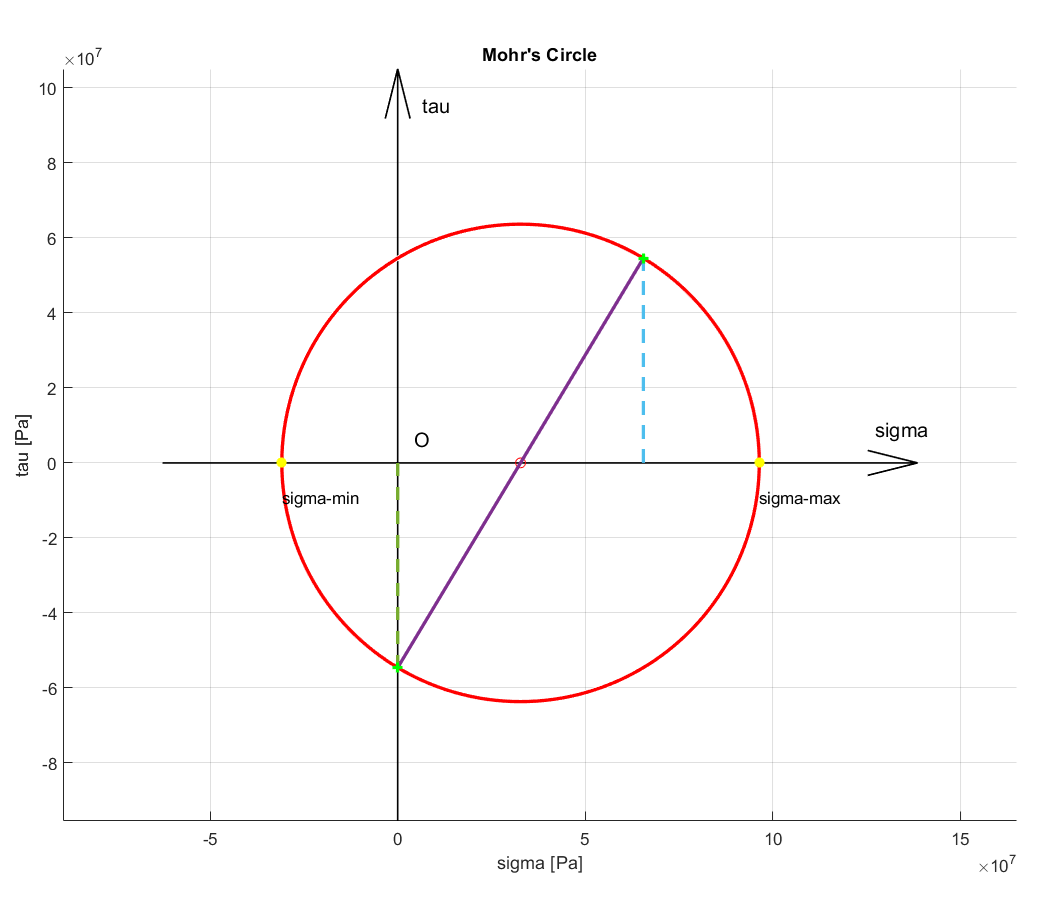
Der Code für die mohr2Ddraw Funktion ist: