Erkennung von Fahrspurlinien mit Hilfe von Echtzeit-Machine-Vision für das Fahrzeugsehen
Die Erkennung von Linien spielt eine entscheidende Rolle bei Anwendungen der maschinellen Bildverarbeitung, z. B. bei der automatischen Erkennung von Fahrspurlinien in autonomen (selbstfahrenden) Fahrzeugen und mobilen Maschinen. Die Aufgabe besteht darin, eine Pipeline zur Erkennung von Liniensegmenten in Fahrspuren aus einem Bild der Straße oder des Weges zusammenzustellen und die funktionierende Pipeline auf einen Videostream anzuwenden.
ZIELE
Erstellung eines Programms in Python zur Erkennung von Straßen- oder Wegspuren in einem Bild und anschließende Anwendung dieser Pipeline auf einen Videostream, der von einer an einem Fahrzeug angebrachten Kamera aufgezeichnet wurde, um darin die Fahrbahngrenzen zu erkennen.
ERWORBENE FÄHIGKEITEN
- Computer-Vision-Techniken mit Python zur Identifizierung von Fahrbahnbegrenzungen in Bildern und Videostreams.
- Verwendung der Bibliotheken OpenCV, NumPy und Matplotlib.
- Bildverarbeitung mit Hilfe von Bildarithmetik.
- Herausfiltern von Bildrauschen und Glätten mit Gauß-Filter.
- Verwendung von Kantenerkennungsalgorithmen zur Identifizierung der Grenzen von Objekten, insbesondere des Canny-Kantendetektors.
- Erstellung eines Algorithmus zur Kantenerkennung.
- Merkmalsextraktion mit Hilfe der Hough-Transformationstechnik.
- Optimierung der extrahierten Merkmale durch Mittelwertbildung.
SCHRITTE
Die hier beschriebene Pipeline zur Fahrspurerkennung ist wie folgt aufgebaut:
- 1. Laden des Bildes
- 2. Kantendetektion
- 3. Region of Interest
- 4. Hough-Transformation
- 5. Optimierung
- 6. Identifizierung von Fahrspurlinien in einem Video
1. Laden des Bildes
In diesem Schritt wird ein Testbild in das Projekt geladen, indem die OpenCV-Bibliothek importiert und ihre Funktion imread() aufgerufen wird, die das Testbild aus einem Ordner liest und es als mehrdimensionales NumPy-Array zurückgibt, das die relativen Intensitäten jedes Pixels im Bild enthält. Dann wird das Testbild mit der Funktion imshow() gerendert, die zwei Argumente entgegennimmt; das erste ist der Name des Fensters (hier: “result”), in dem das image1 (Abbildung 1), das zweite Argument, angezeigt werden soll. Danach folgt die Funktion waitKey(), die eine Dauer von Millisekunden für die Anzeige des Bildes angibt; der Wert $0$ bedeutet, dass das Bild unendlich lange angezeigt wird, bis eine Taste auf der Tastatur gedrückt wird.
import cv2
image1 = cv2.imread('test_image.jpg')
cv2.imshow("result", image1)
cv2.waitKey(0)

2. Kantendetektion
Die Kantenerkennung ist einer der grundlegenden Schritte in der Bildverarbeitung, der Bildanalyse, der Bildmustererkennung und der Computer-Vision-Techniken.
Kanten sind plötzliche Diskontinuitäten in einem Bild. Die Position der Kanten in einem Bild wird anhand des Intensitätsprofils dieses Bildes entlang einer Zeile oder Spalte ermittelt.
Wenn man sich ein Bild als Raster vorstellt, enthält jedes Quadrat im Raster ein Pixel (kurz für picture element), ein Bild ist also eine Kachel (ein Array) aus Pixeln.
Ein digitales Farbbild kann als ein Array von Pixeln (Pixelgitter) dargestellt werden, wobei jedes Pixel drei Kanäle hat und als $1\times3$-Vektor dargestellt wird, der in der Regel aus ganzzahligen Werten besteht und einen RGB-Datenwert (Rot, Grün, Blau) darstellt, der die Farbe, die RGB-Intensitäten (die Lichtmenge) angibt, die an einer bestimmten Stelle des Bildes erscheint. Der minimale Intensitätswert für eine Grundfarbe ist $0$. Die maximale Intensität beträgt $255$. Das bedeutet, dass das Farbmuster eines jeden Pixels drei numerische RGB-Komponenten (Rot, Grün, Blau) hat, die die Farbe dieses winzigen Pixelbereichs darstellen. Diese drei RGB-Komponenten sind drei $8$-Bit-Zahlen für jedes Pixel. Tatsächlich gibt es $256$ (d. h. $8$-Bit-Format; $2^8=256$) verschiedene Intensitätswerte für jede Grundfarbe. Da die drei Farben ganzzahlige Werte von $0$ bis $255$ haben, gibt es insgesamt $256\times256\times256 = 16,777,216$ Kombinationen oder Farbauswahlen. Schwarz hat einen RGB-Wert von $(0, 0, 0)$ und Weiß hat den Wert $(255, 255, 255)$. Grau hat jedoch gleiche RGB-Werte. So ist $(220, 220, 220)$ ein helles Grau (fast weiß) und $(40, 40, 40)$ ein dunkles Grau (fast schwarz).
Da Grau in RGB die gleichen Werte hat, verwenden Schwarz-Weiß-Graustufenbilder nur ein Byte mit $8$-Bit-Daten pro Pixel statt drei. Jedes Pixel hat einen Wert zwischen $0$ und $255$, wobei Null für “keine Intensität” oder “schwarz” und $255$ für “maximale Intensität” oder “weiß” steht. Die Werte gehen allmählich von $0$ bis $255$, was $256$ Graustufen entspricht, von dunkler zu heller. Aus diesem Grund werden in der Bildverarbeitung Farbbilder zur Erkennung von Kanten in Graustufen umgewandelt, da dies zur Vereinfachung der Algorithmen beiträgt und die Komplexität im Zusammenhang mit den Berechnungsanforderungen beseitigt.
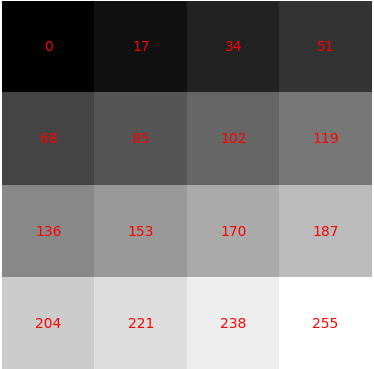
Abbildung 2 zeigt ein Graustufenbild, das in eine Matrix aus quadratischen Formen unterteilt ist, wobei jedes Quadrat aus Pixeln mit einem bestimmten Intensitätswert besteht. Die Intensitätswerte sind in Rot dargestellt. Um dies zu erzeugen, wurde der folgende Python-Code verwendet:
import numpy as np
import matplotlib.pyplot as plt
array = np.array([[0, 17, 34, 51],
[68, 85, 102, 119],
[136, 153, 170, 187],
[204, 221, 238, 255]])
plt.imshow(array, cmap = 'gray')
for i in range(array.shape[0]):
for j in range(array.shape[1]):
plt.text(j,i, str(array[i,j]),color='r', ha='center', va='center')
plt.axis("off")
plt.show()
Hier wurde nach der Definition eines Arrays von Werten das Array geplottet, um ein Graustufenbild anzuzeigen, wobei die Farbkarte mit Hilfe des matplotlib-Parameters cmap='gray' eingerichtet wurde.
Methoden zur Erkennung von Kanten beruhen auf der Berechnung von Bildgradienten, d. h. der Veränderung der Bildintensität in einer bestimmten Richtung. Bereiche in einem Bild, die wie Kanten aussehen, werden durch Messung des Gradienten, d. h. der Änderung der Intensitätswerte, an jedem Pixel des Eingabebildes in einer bestimmten Richtung erkannt. Nach Anwendung eines Kantendetektors auf das Originalbild werden starke Helligkeitsänderungen im Bild erkannt. Im resultierenden Gradientenbild werden die Unstetigkeiten in der Bildhelligkeit durch eine Reihe zusammenhängender Kurven und Linien dargestellt, die die Grenzen der Objekte anzeigen. Diskontinuitäten in der Bildhelligkeit entsprechen Diskontinuitäten in der Tiefe, in der Oberflächenausrichtung, Änderungen der Materialeigenschaften und Variationen in der Szenenbeleuchtung.
Es gibt viele Methoden zur Erkennung von Kanten, darunter Canny, Sobel, Laplacian und Prewitt. Diese lassen sich in zwei Kategorien einteilen: Gradient und Laplacian. Die Gradientenmethode (Canny, Sobel) erkennt die Kanten, indem sie nach dem Maximum und Minimum der ersten Ableitung des Bildes sucht. Die Laplacian-Methode (Laplacian, Prewitt) sucht nach Nulldurchgängen in der zweiten Ableitung des Bildes, um Kanten zu finden. Der * Canny-Algorithmus* (Canny edge detector) ist jedoch der wohl am häufigsten verwendete Kantendetektor in diesem Bereich, da sein Algorithmus eine der am strengsten definierten Methoden ist, die eine gute und zuverlässige Erkennung ermöglicht.
Graustufen-Konvertierung
Die Erkennung von farbigen Kanten wird nur in einigen speziellen Fällen verwendet, da die Berechnungsanforderungen dreimal so hoch sind wie bei Graustufenbildern und die meisten Kanten in Grauwert- und Farbbildern etwa gleich sind.
Bevor der Canny-Algorithmus zur Erkennung von Kanten angewandt wird, werden einige Vorverarbeitungsschritte durchgeführt, beginnend mit dem Importieren der OpenCV- und NumPy-Bibliotheken, dem Einlesen des Bildes mit der Funktion imread() in OpenCV und dem Kopieren des geladenen Bildarrays in eine neue Variable mit der Funktion np.copy() von NumPy, um das Originalbild nicht zu verändern. Es folgt das Einlesen des Farbbildes als Graustufenbild mit der Funktion cvtColor() von OpenCV, die zur Konvertierung des Farbraums eines Bildes verwendet wird. Sie nimmt ein Eingabebild in einem Farbraum und wandelt es in einen anderen Farbraum um; in diesem Fall wird es von RGB in Graustufen umgewandelt, wie im nächsten Code gezeigt.
OpenCV verwendet das BGR-Bildformat (Farbraum). Beim Lesen eines RGB-Bildes mit OpenCV wird das Bild standardmäßig im BGR-Format interpretiert, daher wird cv2.COLOR_BGR2GRAY als Code für die Farbraumkonvertierung verwendet.
import cv2
import numpy as np
image1 = cv2.imread('test_image.jpg')
lane_image = np.copy(image1)
gray_image = cv2.cvtColor(lane_image, cv2.COLOR_BGR2GRAY)
cv2.imshow("result", gray_image)
cv2.waitKey(0)
Das Ergebnis ist in Abbildung 3 dargestellt.

Um den oben erwähnten Unterschied zwischen RGB und BGR schnell zu veranschaulichen, liest der folgende Code ein Bild mit der imread()-Methode von OpenCV ein und stellt es mit dem Matplotlib-Paket sowie der imshow()-Methode von OpenCV dar.
import cv2
import matplotlib.pyplot as plt
image2 = cv2.imread('museum_im_schloss.jpg')
# Using OpenCV
cv2.imshow('Displaying image using OpenCV', image2)
cv2.waitKey(0)
# Using Matplotlib
plt.imshow(image2)
plt.title('Displaying image using Matplotlib')
plt.show()


Der Grund für den Farbunterschied zwischen den beiden Anzeigen ist, dass OpenCV das Bild in BGR- und nicht in RGB-Reihenfolge liest und anzeigt. Matplotlib hingegen verwendet das RGB-Farbformat und erfordert daher, dass das BGR-Bild zuerst in RGB umgewandelt wird, um es korrekt anzuzeigen.
Nun aber zurück zur Graustufen-Konvertierung in OpenCV: Die Konvertierung eines RGB-Bildes in Graustufen ist nicht einfach zu bewerkstelligen. Dies wird durch die Methode des Farbmodus-Ausdrucks realisiert. $R_{i}$, $G_{i}$ und $B_{i}$ stellen die drei Primärfarbwerte jedes Pixels dar, und die Graudaten $C_{i}$ jedes Pixels werden durch Berechnung des Mittelwerts seiner RGB-Daten ermittelt.
Beim menschlichen Sehen sind die Augen jedoch empfindlicher und nehmen daher mehr Grün wahr, weniger empfindlich für Rot und am wenigsten empfindlich für Blau. Daher werden die Gewichte des linearen gewichteten Mittelwerts festgelegt, um die Ungleichmäßigkeit der Empfindlichkeit auszugleichen, und anschließend werden den drei Farben unterschiedliche Gewichte zugewiesen. Die Gewichtungswerte der allgemeinen R-, G- und B-Komponenten betragen $0,299$, $0,587$ bzw. $0,114$.
Bei der Konvertierung in Graustufen wird also nicht jeder der RGB-Kanäle gleichmäßig gewichtet, wie es hier der Fall ist:
\[C_{i} = 0.33 \times R_{i} + 0.33 \times G_{i} + 0.33 \times B_{i}\]Vielmehr wird jeder Kanal unterschiedlich gewichtet, um dem menschlichen Sehvermögen Rechnung zu tragen. Das Konvertierungsmodell kann folgendermaßen ausgedrückt werden:
\[C_{i} = 0.299 \times R_{i} + 0.587 \times G_{i} + 0.114 \times B_{i}\]Canny-Algorithmus zur Kantenerkennung
Der Prozess des Canny-Algorithmus zur Erkennung von Kanten kann in fünf verschiedene Schritte unterteilt werden:
- Rauschunterdrückung durch Glättung des Bildes mit Gauß-Filter
- Ermittlung der Intensitätsgradienten der Pixel im Bild mit dem Sobel-Filter
- Anwendung von Gradientenschwellenwerten oder Non-maximum suppression, um falsche Kanten zu beseitigen
- Anwendung des Doppelschwellenwerts zur Ermittlung potenzieller Kanten
- Kantenverfolgung durch Hysterese: Abschluss der Erkennung von Kanten durch Unterdrückung aller anderen Kanten, die schwach sind und nicht mit starken Kanten verbunden sind.
Schritt 1: Glättung mit Gauß-Filter
Es gibt zwei Hauptarten der Bildverarbeitung: Bildfilterung und Image Warping. Bei der Bildfilterung werden die Pixelwerte eines Bildes geändert, wobei die Farbintensitäten verändert werden, ohne die Pixelpositionen zu verändern, während beim Image Warping die Pixelpositionen eines Bildes verändert werden, ohne die Farben zu verändern.
Nach dem Einlesen des Bildes wird es in einem nächsten Schritt mit der Funktion GaussianBlur() weichgezeichnet. Dies geschieht, um das Rauschen im Bild zu reduzieren, da die meisten Algorithmen zur Kantenerkennung empfindlich auf Rauschen reagieren, und um die Intensitätsschwankungen in der Nähe der Kanten zu glätten, so dass die vorherrschende Kantenstruktur im Bild leichter zu erkennen ist.
Mathematisch gesehen ist die Anwendung eines Gaußschen Weichzeichners auf ein Bild dasselbe wie die Faltung des Bildes mit einer Gaußschen Funktion (die in der Statistik auch die Normalverteilung ausdrückt). Die Werte dieser Verteilung werden verwendet, um eine Faltungsmatrix zu erstellen, die auf das Originalbild angewendet wird. Der neue Wert jedes Pixels wird auf einen gewichteten Durchschnitt der Nachbarschaft dieses Pixels gesetzt. Der Wert des Originalpixels erhält die größte Gewichtung (mit dem höchsten Gauß-Wert), und die benachbarten Pixel erhalten mit zunehmendem Abstand zum Originalpixel kleinere Gewichtungen. Das Ergebnis ist eine Unschärfe, die Grenzen und Kanten besser bewahrt als andere, gleichmäßigere Unschärfefilter. Bei der Faltung wird ein Kernel verwendet und durch ein Eingabebild iteriert, um ein Ausgabebild zu erzeugen.
Bei der Erkennung von Kanten kann das Rauschen dazu führen, dass falsche Kanten im Ergebnis erscheinen. Die Verwendung eines Gaußschen Unschärfefilters vor der Kantenerkennung zielt darauf ab, dieses Rauschen im Bild zu reduzieren, wodurch das Ergebnis des verwendeten Algorithmus zur Kantenerkennung verbessert wird.
Die folgende Codezeile blur = cv2.GaussianBlur(gray,(5,5),0) wendet eine Gaußsche Unschärfe auf das Graustufenbild gray_image mit einem $5\times5$-Kernel und einer Abweichung von Null an und liefert ein neues Bild namens blur_image. Die Größe des Kerns variiert je nach den spezifischen Situationen. Je größer die Größe ist, desto geringer ist die Empfindlichkeit des Detektors gegenüber Rauschen. Außerdem nimmt der Lokalisierungsfehler bei der Erkennung der Kante mit zunehmender Größe des Gaußfilterkerns leicht zu. Ein $5\times5$ ist für die meisten Fälle eine gute Größe.
Der folgende Python-Code wendet den Gaußschen Weichzeichner auf das Graustufenbild eines Weges oder einer Straße an und zeigt das Ergebnis an ( Abbildung 6).
import cv2
import numpy as np
image1 = cv2.imread('test_image.jpg')
lane_image = np.copy(image1)
gray_image = cv2.cvtColor(lane_image, cv2.COLOR_BGR2GRAY)
blur_image = cv2.GaussianBlur(gray_image,(5,5),0)
cv2.imshow("result", blur_image)
cv2.waitKey(0)

Nach der Graustufenkonvertierung und dem Weichzeichnen wird der Canny-Algorithmus nun direkt auf das unscharfe Bild angewendet, indem die Funktion cv2.Canny() im Code aufgerufen wird.
Schritt 2: Berechnung der Intensitätsgradienten
Ein Bild kann als ein Array von Stichproben einer kontinuierlichen Funktion der Bildintensität betrachtet werden. Eine Kante in einem Bild kann in eine Vielzahl von Richtungen zeigen, daher verwendet der Canny-Algorithmus das Konzept der Ableitungen, typischerweise den Sobel-Operator, um sowohl die Größe des Gradienten als auch die Ausrichtung für jedes Pixel zu bestimmen. Die Gradientengröße gibt die Stärke der Intensitätsänderung an; eine kleine Ableitung bedeutet eine kleine Änderung der Intensität, während eine große Ableitung eine große Änderung bedeutet, und die Gradientenorientierung gibt die Richtung der steilsten Änderung an.
Der Sobel-Operator ist ein Operator zur Erkennung von Kanten, der verwendet wird, um den Gradienten oder die Änderungsrate sowohl in der horizontalen (von links nach rechts) als auch in der vertikalen (von oben nach unten) Richtung eines Bildes zu ermitteln. Er gibt einen Wert für die erste Ableitung der kontinuierlichen Funktion der Bildintensität in horizontaler und vertikaler Richtung zurück. Das Ergebnis sind zwei getrennte Gradientenbilder. Durch die Kombination dieser beiden Gradientenbilder werden Kanten und Grenzen im Originalbild identifiziert. Daraus werden für jedes Pixel der Intensitätsgradient * Größe* und Richtung berechnet, wodurch die Intensitätsänderung in Bezug auf benachbarte Pixel gemessen wird.
Schritt 3: Anwenden der Non-maximum suppression
Nach der Rauschunterdrückung und der Berechnung des Intensitätsgradienten (Ermittlung von Gradientengröße und -richtung) besteht der dritte Schritt des Canny-Algorithmus in einer vollständigen Abtastung des Bildes, um alle unerwünschten Pixel zu entfernen (auszudünnen), die nicht unbedingt die Kante darstellen. Dazu wird eine Technik namens Non-Maximum-Suppression von Kanten verwendet, die alle nicht maximalen Pixel in der Gradientenrichtung unterdrückt. Das Ergebnis ist ein Binärbild mit “dünnen Kanten”.
Zu diesem Zweck wird jedes Pixel mit seinen Nachbarpixeln in positiver und negativer Gradientenrichtung verglichen. Ist der Gradientenwert des aktuellen Pixels größer als der seiner Nachbarpixel, wird er unverändert gelassen. Andernfalls wird die Größe des aktuellen Pixels auf Null gesetzt. Dieser Schritt stellt sicher, dass nur die Kanten mit maximaler Intensität erhalten bleiben und die anderen Kanten unterdrückt (auf Null gesetzt) werden.
Schritt 4: Anwendung der doppelten Schwelle
Nach Anwendung der Non-Maximum-Suppression liefern die verbleibenden Kantenpixel eine genauere Darstellung der echten Kanten in einem Bild. Es verbleiben jedoch einige Kantenpixel, die durch Rauschen und Farbvariationen verursacht werden. Um diese falschen Kantenpixel herauszufiltern und echte Kantenpixel zu erhalten, werden hohe und niedrige Schwellenwerte verwendet.
- Kantenpixel mit Gradientenwerten oberhalb des hohen Schwellenwerts werden als starke Kanten markiert, was auf erhebliche Intensitätsänderungen hinweist.
- Kantenpixel, deren Gradient zwischen dem niedrigen und dem hohen Schwellenwert liegt, werden als schwache Kantenpixel gekennzeichnet. Bei diesen schwachen Kantenpixeln kann es sich um echte Kantenpixel oder um Rauschen/Farbvariationen handeln; sie müssen weiter überprüft werden, was wie im nächsten Schritt beschrieben geschieht.
- Kantenpixel mit Gradientenwerten, die kleiner als der niedrige Schwellenwert sind, werden unterdrückt.
Schritt 5: Kantenverfolgung durch Hysterese
Der letzte Schritt des Canny-Algorithmus ist die Kantenverfolgung durch Hysterese. Dieser Algorithmus basiert auf der Idee, dass schwache Kantenpixel von echten Kanten (normalerweise) mit einem starken Kantenpixel verbunden sind, während Rauschreaktionen unverbunden sind. Ausgehend von jedem Pixel einer schwachen Kante verfolgt der Algorithmus die Kante, indem er ihre 8 verbundenen Nachbarpixel berücksichtigt. Wenn mindestens ein Pixel der starken Kante mit einem Pixel der schwachen Kante verbunden ist, wird dieses Pixel der schwachen Kante als eines identifiziert, das erhalten werden sollte. Dieser Prozess wird fortgesetzt, bis keine schwachen Kanten mehr verbunden sind. Diese Pixel mit schwachen Kanten werden zu starken Kanten, die dann dazu führen können, dass ihre benachbarten Pixel mit schwachen Kanten erhalten bleiben. Auf diese Weise wird sichergestellt, dass die Kanten kontinuierlich und gut definiert sind.
Der Python-Code zur Implementierung der oben beschriebenen fünf Schritte des Canny-Algorithmus lautet wie folgt:
import cv2
import numpy as np
image1 = cv2.imread('test_image.jpg')
lane_image = np.copy(image1)
gray_image = cv2.cvtColor(lane_image, cv2.COLOR_BGR2GRAY)
blur_image = cv2.GaussianBlur(gray_image,(5,5),0)
canny_image = cv2.Canny(blur_image, 50, 150)
cv2.imshow("result", canny_image)
cv2.waitKey(0)
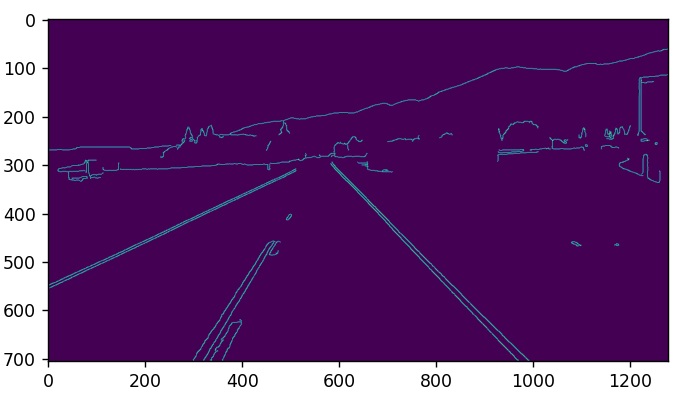
Nach dem Importieren der erforderlichen Python-Pakete wird das Bild geladen und vorverarbeitet. Dann wird der Canny-Algorithmus (Canny edge detector), die Funktion cv2.Canny(), auf das einkanalige Graustufenbild angewendet, um sicherzustellen, dass während des Prozesses weniger Rauschen auftritt. Der erste Parameter für die Funktion cv2.Canny() ist das unscharfe Graustufenbild. Der zweite und dritte Parameter sind der untere bzw. obere Schwellenwert. Schließlich wird das resultierende Bild mit den erkannten Kanten, Abbildung 7, auf dem Bildschirm angezeigt. Es zeigt deutlich die Umrisse der Kanten, die den Pixeln mit den stärksten Intensitätsveränderungen entsprechen. Farbverläufe, die den hohen Schwellenwert überschreiten, werden als helle Pixel nachgezeichnet. Kleine Helligkeitsänderungen werden überhaupt nicht erfasst und sind dementsprechend schwarz, da sie unter den unteren Schwellenwert fallen.

3. Region of Interest
Eine “Region of Interest” (oft abgekürzt als ROI) ist eine Stichprobe innerhalb eines Datensatzes, die für einen bestimmten Zweck bestimmt ist. In der Computer Vision definiert die ROI die Grenzen eines zu betrachtenden Objekts.
Im endgültigen Bild des vorigen Abschnitts, Abbildung 7, ist zu erkennen, dass nach Anwendung des Canny-Algorithmus Kanten im Bild zu erkennen sind, die nicht zu den Fahrspurlinien gehören. Um nur den Bereich zu isolieren, in dem Fahrspurlinien identifiziert werden sollen, wird eine vollständig schwarze Maske mit denselben Abmessungen wie das Originalbild erstellt und ein Teil dieses Bereichs mit einem Polygon gefüllt.
In diesem Projekt ist die Region von Interesse die Fahrspur, auf der sich das Fahrzeug bewegt. Dieser Bereich könnte als Dreieck angegeben werden. Um dies zu erreichen, wird zunächst eine neue Funktion mit dem Namen canny() definiert und der vorherige Code in diese Funktion eingeschlossen. Diese Funktion nimmt als Eingabe ein Bild, wendet den Canny-Algorithmus auf dieses Bild an und gibt das Ergebnisbild als Ausgabe zurück.
Um zu verdeutlichen, wie die “Region of Interest”, die Dimensionen des Dreiecks, isoliert wird, wird anstelle von OpenCV das Unterpaket pyplot des Matplotlib-Pakets verwendet, das die Achsen einer Abbildung anzeigt, wie in Abbildung 8 dargestellt.
import cv2
import numpy as np
import matplotlib.pyplot as plt
def canny(image):
gray_image = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)
blur_image = cv2.GaussianBlur(gray_image,(5,5),0)
canny_image = cv2.Canny(blur_image, 50, 150)
return canny_image
image1 = cv2.imread('test_image.jpg')
lane_image = np.copy(image1)
canny_image = canny(lane_image)
plt.imshow(canny_image)
plt.show()
Dann wird die “Region of Interest”, in der die Fahrspuren identifiziert werden sollen, als Dreieck mit den folgenden drei Eckpunkten $(x,y)$ gezeichnet: $(200px,700px)$, $(1100px,700px)$ und $(550px,250px)$.
Nun wird der vorherige Code umgekehrt, um das Bild mit OpenCV darzustellen, und es wird eine neue Funktion definiert, region_of_interest(), die ein Bild als Eingabe nimmt und die eingeschlossene Region of Interest, die Dreiecksform, zurückgibt. Die Region of Interest wird als 1D NumPy Array von Eckpunkten deklariert.
Die Höhe des Bildes ergibt sich aus der shape()-Funktion des Bildes (2D-Pixelmatrix), die ein Tupel aus zwei ganzen Zahlen $(m, n)$ ist, wobei $m$ die Anzahl der Zeilen ist, was der Höhe des Bildes entspricht, und $n$ die Anzahl der Spalten.
Dieses Polygon wird auf eine schwarze Maske mit denselben Abmessungen wie das Originalbild angewendet. Um dies zu erreichen, wird die Funktion zero_like() von NumPy verwendet, die ein Array mit Nullen derselben Form und desselben Typs wie das Array des Eingabebildes zurückgibt. Diese Maske hat die gleiche Anzahl von Zeilen und Spalten, die gleiche Anzahl von Pixeln und damit die gleichen Abmessungen wie das Originalbild. Ihre Pixel sind jedoch schwarz, da sie eine Intensität von Null haben. Dann wird diese Maske mit dem Dreieck gefüllt, indem die Funktion fillPoly() von OpenCV verwendet wird, die einen durch ein oder mehrere Polygone begrenzten Bereich füllt, d. h. ihr zweiter Parameter ist ein Array von Polygonen (hier: ein Array von einem Polygon). Der dritte Parameter in dieser Funktion gibt die Füllfarbe des Polygons an, die hier als weiß angesehen wird. Auf diese Weise wird der Bereich, der von der definierten Polygonkontur begrenzt wird, mit weißer Farbe gefüllt. Schließlich wird die geänderte Maske als Ausgabe dieser Funktion zurückgegeben, und Abbildung 9 wird auf dem Bildschirm angezeigt.
Dieses Ergebnis wurde durch den folgenden Python-Code erreicht:
import cv2
import numpy as np
def canny(image):
gray_image = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)
blur_image = cv2.GaussianBlur(gray_image,(5,5),0)
canny_image = cv2.Canny(blur_image, 50, 150)
return canny_image
def region_of_interest(image):
height = image.shape[0]
polygons = np.array([
[[200,height],[1100,height],[550,250]]
])
mask = np.zeros_like(image)
cv2.fillPoly(mask, polygons, 255)
return mask
image1 = cv2.imread('test_image.jpg')
lane_image = np.copy(image1)
canny_image = canny(lane_image)
cv2.imshow("result", region_of_interest(canny_image))
cv2.waitKey(0)

Das mask Bild wird nun verwendet, um das canny_image Bild, das Ergebnis des Canny Kantendetektors, zu maskieren, um nur einen bestimmten Bereich dieses Bildes zu zeigen, der durch das Dreieckspolygon nachgezeichnet wird, und die anderen Bereiche zu maskieren.
Dies wird erreicht, indem der bitweise UND-Verknüpfung (&) zwischen dem Ergebnisbild des Canny-Operators und dem Maskenbild angewendet wird. Dieser Operator vergleicht ein Paar von Binärzahlen und ergibt Null, es sei denn, beide Zahlen sind Einsen, wie in der folgenden Tabelle dargestellt:
| A | B | A & B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Der bitweise UND-Operator wird elementweise auf die beiden Bilder angewandt, d. h. auf zwei Pixelreihen, die dieselben Abmessungen und damit dieselbe Anzahl von Pixeln aufweisen. Die elementweise Anwendung des bitweisen UND-Operators wirkt auf jedes homologe Pixel in beiden Reihen und maskiert schließlich das Ergebnisbild des Canny-Kantendetektors, so dass nur der durch das Polygon im Maskenbild nachgezeichnete “region of interest” angezeigt wird.
Das Maskenbild wird zunächst in seiner Pixeldarstellung ausgedruckt, wobei das Dreieckspolygon in Pixelintensitäten von $255$ und die umgebenden Regionen in Pixelintensitäten von $0$ übersetzt werden. Die Binärdarstellung des Wertes $0$ ist $0$ und die Binärdarstellung des Wertes $255$ ist $11111111$ (der maximale Darstellungswert eines $8$-Bit-Bytes; $2^7+2^6+2^5+2^4+2^3+2^2+2^1+2^0 = 255$). Das bedeutet, dass die Umgebung des “ Region of Interest “ schwarz ist und die binäre Darstellung der Intensität jedes Pixels in dieser Region Null ist, da das Ergebnis des bitweisen UND-Operators einer Binärzahl mit allen Nullen mit jeder anderen Binärzahl Nullen ergibt. Das bedeutet, dass alle Pixel in diesem Bereich einen Intensitätswert von Null haben, also schwarz sind, wodurch der gesamte Bereich außerhalb der “Region of Interest” maskiert wird. Im Falle des weißen Polygons wäre die binäre Darstellung der Intensität jedes Pixels in diesem Bereich gleich eins. Das bedeutet, dass die Werte der Pixelintensitäten in diesem Bereich unberührt bleiben, da die Anwendung des bitweisen UND-Operators zwischen allen Einsen und jeder anderen Binärzahl keine Auswirkungen hat.
Dies könnte durch Hinzufügen der OpenCV-Funktion bitwise_and() zur Funktion region_of_interest() im vorherigen Code realisiert werden, die das masked_image Bild als Ergebnis zurückgibt.
import cv2
import numpy as np
def canny(image):
gray_image = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)
blur_image = cv2.GaussianBlur(gray_image,(5,5),0)
canny_image = cv2.Canny(blur_image, 50, 150)
return canny_image
def region_of_interest(image):
height = image.shape[0]
polygons = np.array([
[[200,height],[1100,height],[550,250]]
])
mask = np.zeros_like(image)
cv2.fillPoly(mask, polygons, 255)
masked_image = cv2.bitwise_and(image,mask)
return masked_image
image1 = cv2.imread('test_image.jpg')
lane_image = np.copy(image1)
canny_image = canny(lane_image)
cropped_image = region_of_interest(canny_image)
cv2.imshow("result", cropped_image)
cv2.waitKey(0)
Dies zeigt Abbildung 10, die die isolierte “Region of Interest” aufgrund der Maskierung im Ergebnisbild des Canny-Kantendetektors darstellt.

Der letzte Schritt der Fahrspurerkennung besteht in der Anwendung des Hough-Transformationsalgorithmus, um gerade Linien in der “Region of Interest” zu erkennen und somit die Fahrspur zu identifizieren.
4. Hough-Transformation
In der Computer Vision und der Bildverarbeitung kann ein Kantendetektor als Vorverarbeitungsstufe verwendet werden, um Bildpixel zu erhalten, die auf der gewünschten Kurve, wie Geraden, Kreise oder Ellipsen, im Bildraum liegen. Aufgrund von Mängeln in den Bilddaten oder im Kantendetektor kann es jedoch zu fehlenden Punkten oder Pixeln auf den gewünschten Kurven sowie zu räumlichen Abweichungen zwischen der idealen Linie/dem idealen Kreis/der idealen Ellipse und den verrauschten Kantenpunkten kommen, wie sie vom Kantendetektor erhalten werden.
Wenn beispielsweise Punkte zu einer Linie gehören, wie sieht dann die Linie aus? Wie viele Linien gibt es? Welche Punkte gehören zu welchen Linien?
Um diese Fragen zu beantworten, wird die Hough-Transformation verwendet, um die extrahierten Kantenpunkte zu einer geeigneten Menge von Linien, Kreisen oder Ellipsen zu gruppieren, indem ein explizites Abstimmungsverfahren über eine Menge parametrisierter Bildobjekte durchgeführt wird.
Der einfachste Fall der Hough-Transformation ist die Erkennung gerader Linien. Die Hauptidee ist:
- Aufzeichnung von Stimmen für jede mögliche Linie, auf der jeder Kantenpunkt liegt.
- Suche nach Linien, die viele Stimmen erhalten.
In einem zweidimensionalen Raum wird eine gerade Linie in der Koordinatenebene durch folgende Gleichung dargestellt:
\[y = mx + b\]Diese Linie hat zwei Parameter: $m$ und $b$, wobei $b$ der $y$-Achsenabschnitt der Linie und $m$ die Steigung ist. Diese Linie kann auch in einem Parameterraum, in dem die horizontale Achse die Steigungen und die vertikale Achse die $y$-Achsenabschnitte darstellt, als ein Punkt $(b, m)$ dargestellt werden. Dieser Parameterraum wird auch als Hough-Raum bezeichnet.
Betrachtet man einen einzelnen Punkt $A(x_0,y_0)$ im zweidimensionalen Raum, so gibt es viele mögliche Geraden, die diesen Punkt kreuzen können und jeweils unterschiedliche Werte für $b$ und $m$ haben. Im Parameterraum stellen diese $b$- und $m$-Paare Punkte dar, die sich auf einer Geraden befinden (kollineare Punkte). Ein Punkt $A(x_0,y_0)$ im Bildraum wird also auf eine Linie im Parameterraum (Hough-Raum) abgebildet:
\[b = -x_0m + y_0\]Betrachtet man jedoch zwei Punkte $A(x_0,y_0)$ und $B(x_1,y_1)$ im zweidimensionalen Raum, so gibt es viele mögliche Linien, die jeden Punkt kreuzen können, jede mit unterschiedlichen Werten für $b$ und $m$. Es gibt jedoch eine Linie, die beide Punkte kreuzt. Diese Linie wird im Parameterraum durch einen einzigen Punkt $(b, m)$ dargestellt. Mit anderen Worten: Dieser Punkt im Parameterraum repräsentiert die $(b, m)$-Werte einer Linie im zweidimensionalen Raum, die die beiden Punkte $A(x_0,y_0)$ und $B(x_1,y_1)$ durchkreuzt. Es ist der Schnittpunkt zweier Linien im Hough-Raum:
\(b = –x_0m + y_0\) \(b = –x_1m + y_1\)
Das Gleiche gilt für mehr als zwei Punkte im zweidimensionalen Raum.
Betrachtet man Abbildung 7, das Ergebnisbild der Anwendung des Canny-Kantendetektors, und nimmt einige Punkte, zum Beispiel $A$, $B$, $C$ und $D$ in diesem zweidimensionalen Bildraum, so gibt es viele Linien, die jeden dieser Punkte durchkreuzen können. Im Parameterraum, dem Hough-Raum, werden die Linien, die z.B. $A$ durchkreuzen, durch Punkte mit jeweils spezifischen $b$- und $m$-Werten, $y$-Achsenabschnitt und Steigungswerten dargestellt, und diese Punkte liegen auf einer Geraden (kollineare Punkte) im Parameterraum. Das gleiche gilt für die Punkte $B$, $C$ und $D$. Auf diese Weise gibt es vier Linien im Parameterraum, die alle Linien im zweidimensionalen Raum repräsentieren, die die vier Punkte $A$, $B$, $C$ und $D$ durchkreuzen. Der Schnittpunkt der Linien im Parameterraum, ein Punkt $(b, m)$, stellt eine Linie mit den Parametern $(b, m)$ dar, die alle vier Punkte $A$, $B$, $C$ und $D$ im zweidimensionalen Raum, dem Bildraum, durchkreuzt. Diese Idee der Identifizierung möglicher Linien aus einer Reihe von Punkten ist die Art und Weise, wie Linien im Bild identifiziert werden.
Vertikale Linien stellen jedoch ein Problem dar. Sie würden zu unendlichen Werten für den Steigungsparameter $m$ führen. Daher wird die Gerade $y = mx + b$ aus rechnerischen Gründen nicht mit den Parametern $m$ und $b$ des kartesischen Koordinatensystems ausgedrückt, sondern im Polarkoordinatensystem mit den Parametern $r$ und $\theta$ und der Geradengleichung:
Dabei ist $r$ der Abstand vom Ursprung zum nächstgelegenen Punkt auf der Geraden, d. h. der senkrechte Abstand, und $\theta$ ist der Winkel zwischen der $x$-Achse und der Verbindungslinie zwischen dem Ursprung und dem nächstgelegenen Punkt, der im Uhrzeigersinn zunimmt.
Für eine vertikale Linie im zweidimensionalen Raum gilt zum Beispiel $\theta = 0$ ⇒ $r=x\cos 0 +y\sin 0 = x$. Für eine horizontale Linie im zweidimensionalen Raum, $\theta = 90°$ ⇒ $r=x\cos \frac{\pi}{2} +y\sin \frac{\pi}{2} = y$.
Bei der Darstellung einer Linie im Polarkoordinatensystem können für jeden Punkt $(x,y)$ im Bildraum mehrere Linien diesen Punkt durchkreuzen, die jeweils im Polarkoordinatensystem (hier: Hough-Raum) mit einem Punkt $(\theta,r)$ dargestellt werden können. Die Menge aller Geraden, die den Punkt $(x,y)$ kreuzen, entspricht einer Sinuskurve in der Ebene $(\theta,r)$, die für diesen Punkt eindeutig ist. Eine Menge von zwei oder mehr Punkten, die eine Gerade bilden, erzeugt Sinuskurven, die sich im $(\theta,r)$ für diese Gerade durchkreuzen. Somit kann das Problem der Erkennung kollinearer Punkte im Hough-Raum in das Problem der Suche nach konkurrierende (sich in einem Punkt schneidende) Kurven im Hough-Raum umgewandelt werden.
Genau wie zuvor, wenn sich die Kurven verschiedener Punkte im Bildraum im Hough-Raum kreuzen, dann gehören diese Punkte zu derselben Linie im zweidimensionalen Raum und sind durch ein bestimmtes $(\theta,r)$ gekennzeichnet. Je mehr Kurven sich im Hough-Raum schneiden, desto mehr Punkte im Bildraum werden von der Linie durchkreuzt, die durch diesen Schnittpunkt repräsentiert wird.
Das bedeutet, dass eine Linie im Allgemeinen durch die Anzahl der Schnittpunkte zwischen Kurven im Hough-Raum (in der $\theta$ - $r$-Ebene) erkannt werden kann. Je mehr Kurven sich kreuzen, desto mehr Punkte hat die Linie, die durch diesen Schnittpunkt repräsentiert wird. Im Allgemeinen kann man einen Schwellenwert für die Mindestanzahl der sich kreuzenden Kurven festlegen, die erforderlich ist, um eine Linie zu erkennen.
Aufgrund von Unzulänglichkeiten in den Bilddaten oder im Kantendetektor kann es jedoch zu fehlenden Punkten oder Pixeln auf den gewünschten Linien im Bildraum sowie zu räumlichen Abweichungen zwischen der Ideallinie und den verrauschten Kantenpunkten kommen, wie sie vom Kantendetektor ermittelt werden. Dies führt dazu, dass sich die Kurven im Polarraum in mehr als einem Punkt in der Nähe kreuzen. Der Zweck der Hough-Transformation ist es, dieses Problem zu lösen, indem sie die Gruppierung von Kantenpunkten zu Linienkandidaten durch ein explizites Abstimmungsverfahren ermöglicht. Welche Linie passt am besten zu mehreren Kantenpunkten im Bildraum? Diese Punkte haben Kurven im Polarraum, wobei jede Kurve die Linien darstellt, die einen einzelnen Punkt dieser Punkte durchkreuzen.
Um die Linie der besten Anpassung für diese Punkte zu finden, wird der Hough-Raum (hier: der Polarraum) in ein Raster aufgeteilt, wobei jeder Behälter innerhalb dieses Rasters einem Winkel $\theta$ und einem Abstand $r$ einer Kandidatenlinie entspricht. Aufgrund der Unzulänglichkeiten können sich mehrere Schnittpunkte innerhalb eines einzigen Behälters befinden (ein einzelner Behälter repräsentiert eine Linie im Bildraum). Dann wird für jeden Schnittpunkt innerhalb eines Behälters ein Abstimmungsverfahren innerhalb des Behälters durchgeführt, zu dem er gehört. Jeder Kantenpunkt im Bildraum stimmt für eine Reihe von möglichen Parametern im Hough-Raum ab. Die Stimmen werden in diskreten Behältern akkumuliert. Der Behälter mit den meisten Stimmen (d. h. der Behälter mit der größten Anzahl von Schnittpunkten) wird die Linie im Bildraum sein, die sich mit diesen Punkten kreuzt. Der Zweck dieser Technik ist es, Unzulänglichkeiten von Punkten im Bildraum und die Linie, zu der sie gehören, zu finden, da das Abstimmungsverfahren für die Linie der besten Anpassung stimmt (die Linie, die $\theta$ und $r$ Werte des Behälters hat).
Der grundlegende Hough-Transformationsalgorithmus, beispielsweise für ein Bild mit einer Linie, nimmt den ersten Punkt der Linie. Die $(x,y)$-Werte dieser Linie im Bildraum sind bekannt. In die Geradengleichung werden die Werte von $\theta = 0,1,2,….,180$ eingesetzt und der Wert von $r$ wird berechnet. Für jedes $(\theta,r)$-Paar wird der Wert der Stimme in den entsprechenden $(\theta,r)$-Bins um eins erhöht.
Dann nimmt der Algorithmus den zweiten Punkt auf der Linie. Er tut dasselbe wie oben. Er erhöht die Werte in den Bins, die der Resultierenden $(\theta,r)$ entsprechen. Diesmal wird das Feld, das zuvor gewählt wurde, ein zweites Mal gewählt, also wird sein Wert erhöht. Damit werden die $(\theta,r)$-Werte abgestimmt. Dieser Vorgang wird für jeden Punkt auf der Linie fortgesetzt. An jedem Punkt wird der Wert desselben Feldes inkrementiert oder hochgestuft, während andere Felder hochgestuft werden können oder auch nicht. Auf diese Weise hat dieser Bereich am Ende die meisten Stimmen und zeigt an, dass es in diesem Bild eine Linie im Abstand $r$ vom Ursprung und im Winkel $\theta$ gibt.
In OpenCV kann die Hough Linien Transformation auf zwei Arten implementiert werden: Eine Standard Hough Linien Transformation und eine * Probabilistische Hough Linien Transformation. Die *Standard Hough Linien Transformation wird mit der Funktion HoughLines() implementiert, es ist die bisher erklärte Operation. Sie liefert als Ergebnis einen Vektor der Paare $(\theta,r)$. Die Probabilistische Hough Linien Transformation ist dagegen eine effizientere Implementierung der Hough Linien Transformation. Sie liefert als Ausgabe die Extremwerte der erkannten Linien $(x_{start}, y_{start}, x_{end}, y_{end})$. In OpenCV ist sie mit der Funktion HoughLinesP() implementiert.
Um mit dem vorherigen Code fortzufahren, wird nach der Erkennung der Bildkanten mit Hilfe eines Canny-Detektors die Probabilistische Hough Linien Transformation angewendet, die folgende Syntax hat:
linesP = cv2.HoughLinesP(image, 2, np.pi / 180, 100, np.array([]), minLineLength=40, maxLineGap=5)
mit den folgenden Parametern:
image: Das Bild, in dem die Linien erkannt werden sollen, dascropped_imageBild.linesP: Ein Vektor, der die Parameter $(x_{start}, y_{start}, x_{end}, y_{end})$ der erkannten Linien speichert.
Die nächsten beiden Argumente geben die Auflösung des Hough-Akkumulator-Arrays an, das zuvor als Gitter beschrieben wurde, ein Array aus Zeilen und Spalten, das die Bins enthält, die zur Akkumulation der Stimmen verwendet werden. Jedes Feld steht für einen bestimmten Wert von $\theta$ und $r$. Die nächsten beiden Argumente geben die Größe der Bins an. Je größer die Bins sind, desto ungenauer werden die erkannten Linien sein und umgekehrt. Zu kleine Bins können jedoch zu Ungenauigkeiten führen und benötigen mehr Zeit für die Ausführung.
r: Die Auflösung des Parameters $r$ in Pixeln. Hier verwendet $2$ Pixel.theta: Die Auflösung des Parameters $\theta$ in Radiant. Hier verwendet $1$ Grad Genauigkeit in Radiant, d.h.(np.pi/180)threshold: Die Mindestanzahl der Stimmen (Kreuzungen) in einem Behälter, um eine Linie zu “entdecken”, d. h. um eine Kandidatenlinie zu akzeptieren. Hier wurde $100$ gewählt, was bedeutet, dass die Mindestanzahl der Schnittpunkte im Hough-Raum für einen Behälter $100$ betragen muss, damit er als relevante Linie zur Beschreibung der Daten (der Kantenpunkte) akzeptiert wird.- Ein leeres Platzhalter-Array.
minLineLength: Die Mindestanzahl der Punkte (Pixel), die eine Linie bilden können. Linien mit weniger als dieser Anzahl von Punkten werden nicht berücksichtigt.maxLineGap: Der maximale Abstand zwischen zwei Punkten (Pixeln), die als in einer Linie liegend betrachtet werden und somit verbunden und nicht getrennt (unterbrochen) sind.
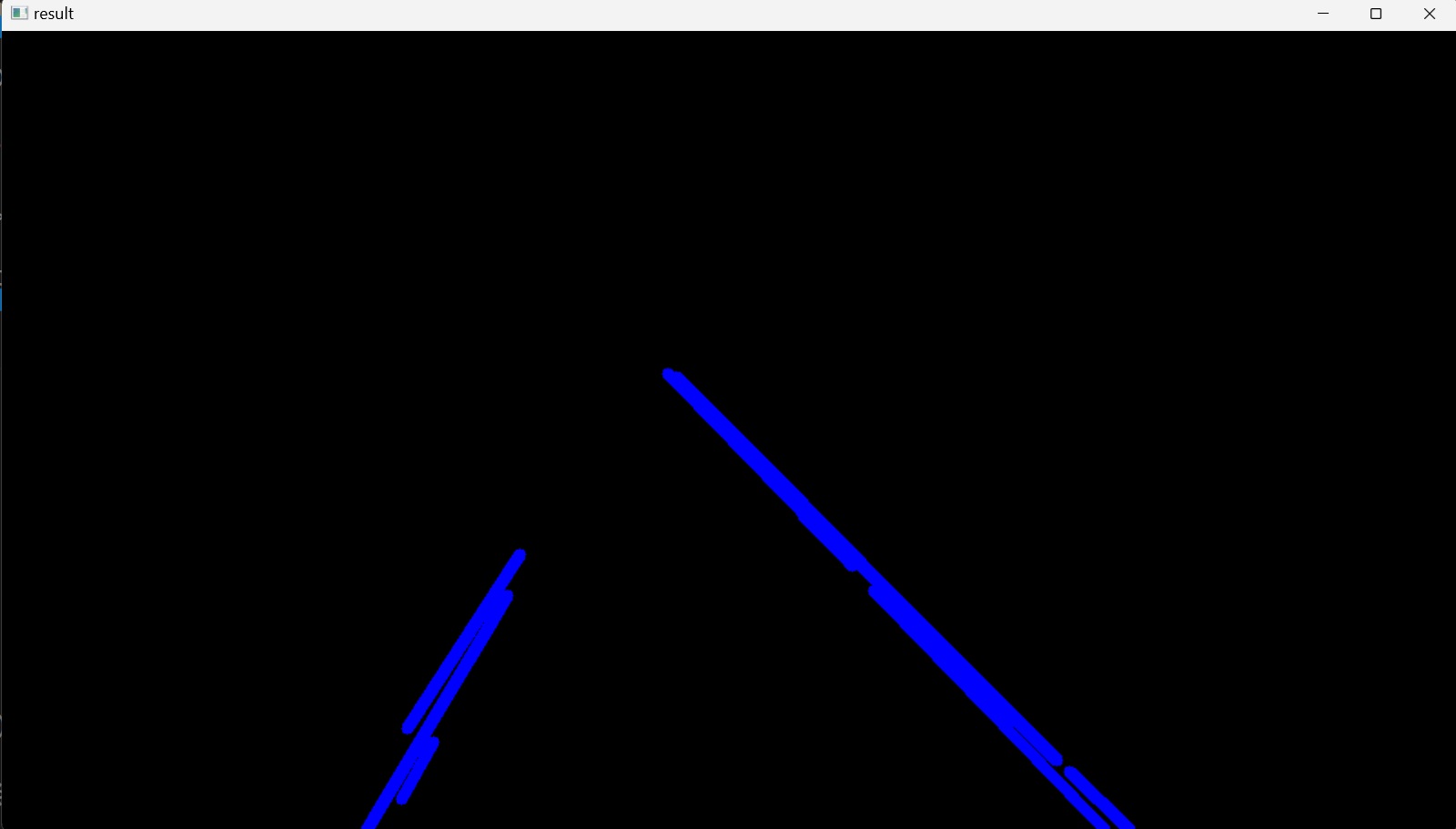
Nach der Einstellung des Algorithmus für die Hough-Linien-Transformation besteht der nächste Schritt darin, die erkannten Linien im Originalbild darzustellen, indem sie gezeichnet werden. Zu diesem Zweck wird eine neue Funktion, display_lines(), definiert, die zwei Eingaben benötigt: Ein Bild, in diesem Fall das lane_image, auf dem die Linien dargestellt werden sollen, sowie die Linien selbst, linesP.
In der Funktion display_lines() wird die NumPy-Funktion zero_like() verwendet, die ein Array von Nullen mit der gleichen Form (Abmessungen) und dem gleichen Typ wie das Array des Eingabebildes zurückgibt. Dann werden alle Linien, die zuvor durch die Hough-Linien-Transformation erkannt wurden, auf diesem schwarzen Bild angezeigt. Um dies zu erreichen, wird zunächst geprüft, ob das Array nicht leer ist; dass lines is not None, dann wird es durch die lines durchlaufen, was ein dreidimensionales Array ist, das aus den Linien und den entsprechenden zweidimensionalen Zeilen, $1\times4$, Vektoren besteht; die $(x_{start}, y_{start}, x_{end}, y_{end})$ Parameter jeder Linie. Dann wird jedes zweidimensionale Array, die Parameter jeder Zeile, in ein eindimensionales Array mit vier Elementen umgewandelt, gefolgt von der Zuweisung dieser Elemente an vier verschiedene Variablen $x_{1}, y_{1}, x_{2},$ and $y_{2}$. Schließlich wird jede Linie, die die for-Schleife durchlaufen hat, mit Hilfe der OpenCV-Funktion line(image, start_point, end_point, line_color, line_thickness) auf das schwarze Bild line_image gezeichnet.
Auf diese Weise werden alle Linien, die mit Hilfe des Canny-Kantendetektors erkannt wurden, auf ein schwarzes Bild gezeichnet ( Abbildung 11).
Der Python-Code für diesen Abschnitt sieht wie folgt aus:
import cv2
import numpy as np
def canny(image):
gray_image = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)
blur_image = cv2.GaussianBlur(gray_image,(5,5),0)
canny_image = cv2.Canny(blur_image, 50, 150)
return canny_image
def display_lines(image, lines):
line_image = np.zeros_like(image)
if lines is not None:
for line in lines:
x1, y1, x2, y2 = line.reshape(4)
cv2.line(line_image,(x1,y1),(x2,y2),(255,0,0),10)
return line_image
def region_of_interest(image):
height = image.shape[0]
polygons = np.array([
[[200,height],[1100,height],[550,250]]
])
mask = np.zeros_like(image)
cv2.fillPoly(mask, polygons, 255)
masked_image = cv2.bitwise_and(image,mask)
return masked_image
image1 = cv2.imread('test_image.jpg')
lane_image = np.copy(image1)
canny_image = canny(lane_image)
cropped_image = region_of_interest(canny_image)
linesP = cv2.HoughLinesP(cropped_image, 2, np.pi / 180, 100, np.array([]), minLineLength=40, maxLineGap=5)
line_image = display_lines(lane_image,linesP)
cv2.imshow("result", line_image)
cv2.waitKey(0)
Schließlich wird das Bild der erkannten Linien, das auf einem schwarzen Bild (Abbildung 11) angezeigt wird, in das ursprüngliche Farbbild (Abbildung 1) eingeblendet, um die Linien auf den Fahrspuren zu zeigen. Dazu wird eine Variable blended_image erstellt und ihr das Ausgabe-Array der OpenCV-Funktion addWeighted(src1, alpha, src2, beta, gamma[, dst[, dtype]]) zugewiesen, das die gleiche Größe und Anzahl von Kanälen wie die Eingabe-Arrays hat: das ursprüngliche Farbbild, lane_image, und das line_image, und sie werden durch die gewichtete Summe zwischen den Arrays dieser beiden Bilder gemischt. Dem lane_image wird eine Gewichtung von $0.8$ zugewiesen, um die Pixelintensitäten zu reduzieren und sie etwas dunkler zu machen, und dem line_image wird eine Gewichtung von $1$ zugewiesen, entsprechend dem folgenden Matrixausdruck:
Dabei ist $dst$ die Ausgangsmatrix und $gamma$ ein Skalar, der zu jeder Summe addiert wird. Dementsprechend hat das line_image durch das Überblenden dieser beiden Bilder $20\%$ mehr Gewicht und ist im blended_image klarer definiert.
Auf diese Weise werden alle Linien, die mit dem Canny-Kantendetektor erkannt wurden, auf ein schwarzes Bild gezeichnet und dann in das ursprüngliche Farbbild eingefügt, so dass die erkannten Linien über den entsprechenden Fahrspurlinien im Originalbild angezeigt werden (Abbildung 12). Der Python-Code für diesen Abschnitt sieht wie folgt aus:
import cv2
import numpy as np
def canny(image):
gray_image = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)
blur_image = cv2.GaussianBlur(gray_image,(5,5),0)
canny_image = cv2.Canny(blur_image, 50, 150)
return canny_image
def display_lines(image, lines):
line_image = np.zeros_like(image)
if lines is not None:
for line in lines:
x1, y1, x2, y2 = line.reshape(4)
cv2.line(line_image,(x1,y1),(x2,y2),(255,0,0),10)
return line_image
def region_of_interest(image):
height = image.shape[0]
polygons = np.array([
[[200,height],[1100,height],[550,250]]
])
mask = np.zeros_like(image)
cv2.fillPoly(mask, polygons, 255)
masked_image = cv2.bitwise_and(image,mask)
return masked_image
image1 = cv2.imread('test_image.jpg')
lane_image = np.copy(image1)
canny_image = canny(lane_image)
cropped_image = region_of_interest(canny_image)
linesP = cv2.HoughLinesP(cropped_image, 2, np.pi / 180, 100, np.array([]), minLineLength=40, maxLineGap=5)
line_image = display_lines(lane_image,linesP)
blended_image = cv2.addWeighted(lane_image, 0.8,line_image,1, 1)
cv2.imshow("result", blended_image)
cv2.waitKey(0)

5. Optimierung
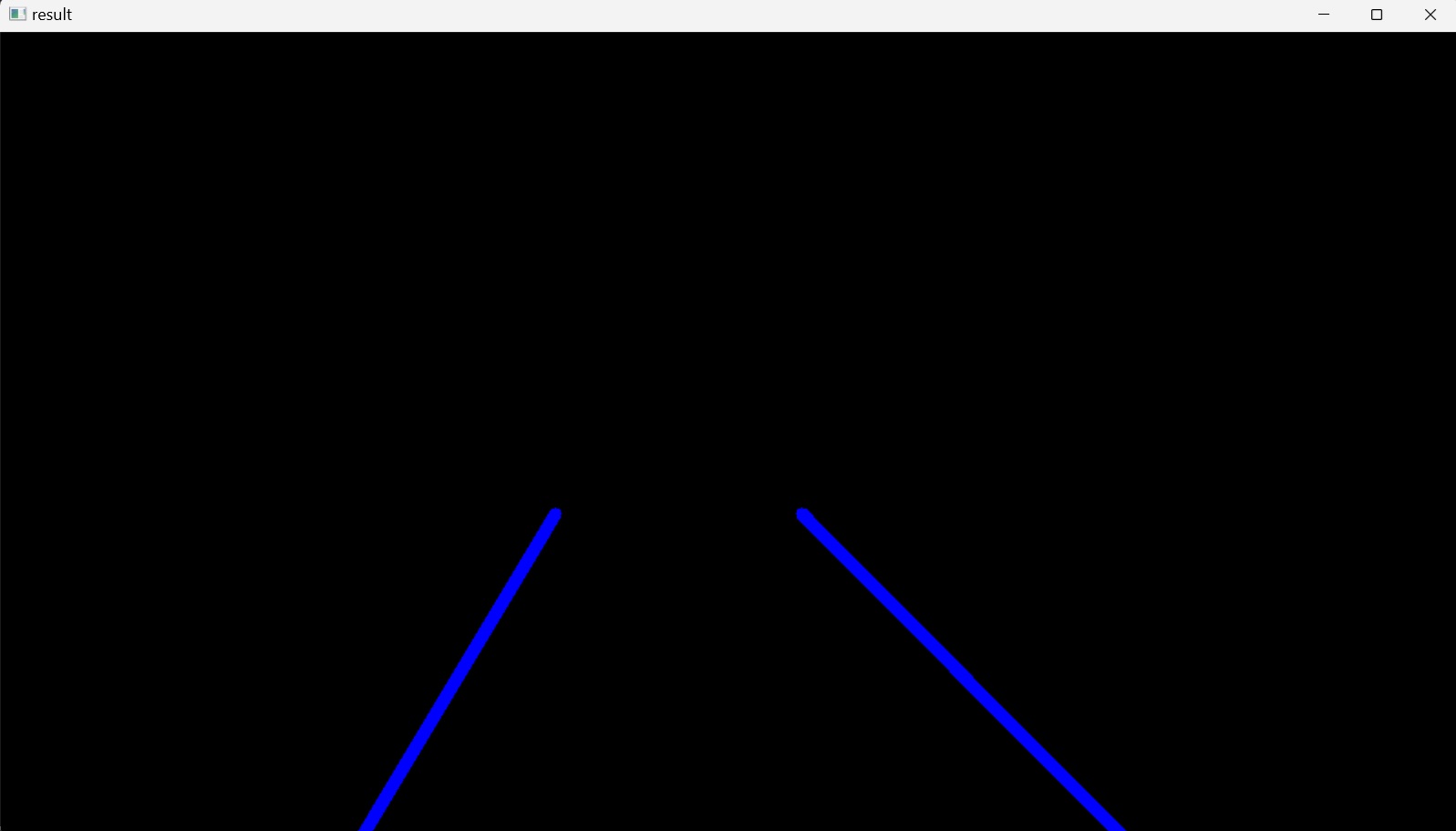
Die mehreren Linien, die auf jeder Fahrspur im Originalbild angezeigt werden, könnten weiter optimiert werden, indem die Steigung und der $y$-Achsenabschnitt dieser mehreren Linien zu einer einzigen Linie gemittelt werden, die beide Fahrspurlinien nachzeichnet.
Zu diesem Zweck wird eine neue Funktion definiert: average_slope_intercept(), die zwei Bilder als Eingabe benötigt. Das ursprüngliche farbige Bild lane_image und die erkannten Linien linesP werden an diese Funktion übergeben, indem eine neue Variable averaged_lines definiert wird, die dem Rückgabewert dieser Funktion entspricht. Innerhalb der Funktionsdefinition werden zwei leere Listen deklariert, left_fit und right_fit, die die Koordinaten der gemittelten Linien enthalten, die auf der linken bzw. rechten Seite der Fahrspur in der “Region of Interest” angezeigt werden. Dazu wird durch jede Zeile iteriert und jede Zeile in ein eindimensionales Array mit vier Elementen umgewandelt, denen jeweils die Variablen $x_{1}, y_{1}, x_{2},$ und $y_{2}$ zugewiesen werden. Dies sind die Anfangs- und Endpunkte einer Linie im zweidimensionalen Bildraum, benötigt werden aber die Steigung und der $y$-Achsenabschnitt dieser Linie. Um diese Werte zu ermitteln, wird eine neue Variable, parameters, auf die Rückgabewerte der NumPy-Funktion np.polyfit() gesetzt, die ein Polynom ersten Grades (eine Linie) an die Punkte $(x_{1}, y_{1})$ und $(x_{2}, y_{2})$ anpasst und einen Vektor von Koeffizienten zurückgibt, die die Steigung und den $y$-Achsenabschnitt der Linie beschreiben, das erste bzw. zweite Element des Vektors.
Die Funktion np.polyfit() benötigt drei Parameter: die $y$- und $x$-Werte der zuvor definierten Start- und Endpunkte sowie eine ganze Zahl, hier: $1$, die den Grad des Polynoms zur Anpassung der Punkte definiert. Dementsprechend werden die Parameter der linearen Funktion ermittelt und den Variablen slope und y_intercept zugewiesen. Anschließend wird nach jeder Iteration geprüft, ob die jeweilige Linie einer Linie auf der linken oder rechten Seite der Fahrspur entspricht. Es ist wichtig zu beachten, dass im OpenCV-Koordinatensystem die $Y$-Achse nach unten gerichtet ist. Außerdem hat eine Linie nach der Definition der Steigung eine positive Steigung, wenn ihre $y$-Werte mit zunehmenden $x$-Werten steigen. Auf den Bildern ist zu erkennen, dass alle Linien in der interessierenden Region in die gleiche Richtung verlaufen, entweder etwas schräg nach links, auf der rechten Seite der Fahrbahn (positiver Steigungswert), oder etwas schräg nach rechts, auf der linken Seite der Fahrbahn (negativer Steigungswert). Auf dieser Grundlage werden Linien mit positiver Steigung an die Liste right_fit und Linien mit negativer Steigung an die Liste left_fit angehängt.
Die appended-Methode von Python nimmt ein einzelnes Argument als Eingabe, ein Element, und fügt dieses Element an das Ende der Liste an. In diesem Fall sind die den Listen hinzugefügten Elemente Tupel (slope, y_intercept), so dass beide Listen die Form einer Matrix mit mehreren Zeilen und zwei Spalten haben. Am Ende der Iteration der $for$-Schleife werden die Werte in jeder Liste mit Hilfe der NumPy-Funktion average() zu einer einzigen Steigung und einem $y$-Achsenabschnitt gemittelt, die den Durchschnitt entlang der angegebenen Achse zurückgeben. In diesem Fall nimmt sie als Eingabe eine Liste und gibt den Durchschnitt dieser Liste entlang der ersten Achse, die senkrecht nach unten über die Zeilen verläuft (Achse $0$), zurück. Das Ergebnis sind zwei Arrays, die jeweils die durchschnittliche Steigung und den $y$-Achsenabschnitt einer einzelnen Linie auf der linken bzw. rechten Seite der Fahrspur darstellen.
Nachdem die Steigungen und $y$-Achsenabschnitte der linken und rechten Linie ermittelt wurden, müssen im nächsten Schritt die Koordinaten angegeben werden, an denen die Linien platziert werden sollen: $x_{1}, y_{1}, x_{2},$ und $y_{2}$ für jede Linie. Dazu wird eine neue Funktion definiert, make_coordinates(), die die Argumente image und line_parameters als Eingabe hat. line_parameters sind die Steigung und der $y$-Achsenabschnitt der linken und der rechten Linie, in diesem Fall der left_fit_average und der right_fit_average, jeweils eine Liste mit zwei Elementen; ein Steigungswert und ein $y$-Achsenabschnitt. Dann werden die Anfangs- und Endpunkte der Linien durch die Einstellung y1 = image.shape[0] festgelegt, wobei die Methode shape() einen Tupelwert zurückgibt, der die Länge der entsprechenden Array-Dimensionen angibt, d. h. die Anzahl der entsprechenden Elemente. In diesem Fall setzt y1 = image.shape[0] die Anzahl der Bildpixel nur entlang der vertikalen $Y$-Achse, die nach unten gerichtet ist, gleich y1. $y_2$ wird auf das $\frac{3}{5}$-fache der Länge von $y_1$ gesetzt. Das bedeutet, dass beide Linien am unteren Rand des Bildes beginnen und drei Fünftel der Strecke nach oben verlaufen. $x_1$ und $x_2$ werden algebraisch aus der Gleichung der jeweiligen Linie bestimmt.
Nachdem alle Koordinaten ermittelt wurden, wird das Ergebnis der Funktion make_coordinates() als NumPy-Array an die beiden Aufrufer left_line und right_line innerhalb der Funktion average_slope_intercept() zurückgegeben. Dann wird das Ergebnis der Funktion average_slope_intercept(), die beiden gemittelten Linien, als NumPy-Array an den Aufrufer, die Variable averaged_lines, zurückgegeben.
Schließlich wird averaged_lines an die Variable line_image anstelle der zuvor übergebenen linesP übergeben, und das Ergebnis line_image wird durch die Codezeile cv2.imshow("result", line_image) auf dem Bildschirm angezeigt, Abbildung 13.
Um das überblendete Bild der gemittelten Linien in das Originalbild (Abbildung 13) zu zeigen, wird die Codezeile cv2.imshow("result", line_image) in cv2.imshow("result", blended_image) geändert.

Hier könnte der Code verbessert werden, indem der Code der zuvor definierten Funktion display_lines() geändert wird:
def display_lines(image, lines):
line_image = np.zeros_like(image)
if lines is not None:
for line in lines:
x1, y1, x2, y2 = line.reshape(4)
cv2.line(line_image,(x1,y1),(x2,y2),(255,0,0),10)
return line_image
durch Entfernen der Codezeile x1, y1, x2, y2 = line.reshape(4) in der for-Schleife und Ersetzen des Werts line, die bei jeder Iteration auf jeden Wert von lines zugreift, durch x1, y1, x2, y2. Dies ist nun möglich, da die Umformung oder Abflachung jeder Zeile bereits in der Funktion average_slope_intercept() erfolgt. Es besteht also keine Notwendigkeit, jede line in der Funktion display_lines() erneut zu formen oder zu glätten. Der Code der Funktion display_lines() wird also geändert in:
def display_lines(image, lines):
line_image = np.zeros_like(image)
if lines is not None:
for x1, y1, x2, y2 in lines:
cv2.line(line_image,(x1,y1),(x2,y2),(255,0,0),10)
return line_image
Der endgültige Code für diesen Abschnitt ist wie folgt:
import cv2
import numpy as np
def make_coordinates(image, line_parameters):
slope, y_intercept = line_parameters
y1 = image.shape[0]
y2 = int(y1*(3/5))
x1 = int((y1 - y_intercept)/slope)
x2 = int((y2 - y_intercept)/slope)
return np.array([x1, y1, x2, y2])
def average_slope_intercept(image, lines):
left_fit = []
right_fit = []
for line in lines:
x1, y1, x2, y2 = line.reshape(4)
parameters = np.polyfit((x1, x2), (y1, y2), 1)
slope = parameters[0]
y_intercept = parameters[1]
if slope < 0:
left_fit.append((slope, y_intercept))
else:
right_fit.append((slope, y_intercept))
left_fit_average = np.average(left_fit, axis=0)
right_fit_average = np.average(right_fit, axis=0)
left_line = make_coordinates(image, left_fit_average)
right_line = make_coordinates(image, right_fit_average)
return np.array([left_line, right_line])
def canny(image):
gray_image = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)
blur_image = cv2.GaussianBlur(gray_image,(5,5),0)
canny_image = cv2.Canny(blur_image, 50, 150)
return canny_image
def display_lines(image, lines):
line_image = np.zeros_like(image)
if lines is not None:
for x1, y1, x2, y2 in lines:
cv2.line(line_image,(x1,y1),(x2,y2),(255,0,0),10)
return line_image
def region_of_interest(image):
height = image.shape[0]
polygons = np.array([
[[200,height],[1100,height],[550,250]]
])
mask = np.zeros_like(image)
cv2.fillPoly(mask, polygons, 255)
masked_image = cv2.bitwise_and(image,mask)
return masked_image
image1 = cv2.imread('test_image.jpg')
lane_image = np.copy(image1)
canny_image = canny(lane_image)
cropped_image = region_of_interest(canny_image)
linesP = cv2.HoughLinesP(cropped_image, 2, np.pi / 180, 100, np.array([]), minLineLength=40, maxLineGap=5)
averaged_lines = average_slope_intercept(lane_image, linesP)
line_image = display_lines(lane_image, averaged_lines)
blended_image = cv2.addWeighted(lane_image, 0.8,line_image,1, 1)
cv2.imshow("result", blended_image)
cv2.waitKey(0)
6. Identifizierung von Fahrspurlinien in einem Video
In den vorangegangenen Abschnitten wurde der Algorithmus zur Erkennung von Fahrspurlinien entwickelt und erfolgreich zur Identifizierung von Fahrspurlinien in einem Bild eingesetzt. In diesem Abschnitt wird derselbe Algorithmus zur Erkennung von Fahrspurlinien in einem Video verwendet.
Um das Video in den Arbeitsbereich aufzunehmen, wird die Funktion VideoCapture() von OpenCV verwendet, deren Argument entweder der Index der Kamera (beginnend mit $0$ für die erste Kamera) oder der Name einer Videodatei ist. Hier wird eine zuvor aufgezeichnete Videodatei verwendet. Diese Funktion gibt ein VideoCapture-Objekt cap zurück.
Ein Video ist eine Sammlung von Bildern, “Frames”. Um einen Videostrom zu verarbeiten, durchläuft das Programm alle Bilder der Videosequenz in einer Schleife und verarbeitet sie dann nacheinander.
Dazu wird eine unendliche while-Schleife eingerichtet, die nach der Initialisierung des VideoCapture-Objekts cap.isOpen() mit Hilfe der read()-Methode jedes aufeinanderfolgende Videobild aus dem cap-Objekt liest (erfasst und dekodiert) und ein Tupel zurückgibt, bei dem das erste Element ein Boolean und das nächste Element das aktuelle Videobild ist. Wenn das erste Element, success, True ist, was bedeutet, dass das Lesen erfolgreich war, wird das zweite Element, das aktuelle Bild im Video, zurückgegeben und der Variablen frame1 zugewiesen. Nachdem überprüft wurde, dass die Bedingung der nächsten if-Anweisung False ist, wird frame1 einer neuen Variablen namens frame zugewiesen, und der Wert dieser Variablen wird durch den Algorithmus zur Kantenerkennung geleitet. Der Grund für diesen zusätzlichen Schritt und die nicht direkte Übergabe von frame1 an den Algorithmus ist, dass die read()-Methode innerhalb der while-Schleife am Ende des Videos ein leeres Videobild an den Algorithmus übergibt, da es keine weiteren Bilder mehr gibt, und dies eine Fehlermeldung im Terminalfenster verursacht: _src.empty() in function 'cv::cvtColor'. Um dies zu vermeiden, wird die if-Anweisung zur Überprüfung des booleschen Werts hinzugefügt, so dass die Schleife unterbrochen wird, wenn der success z. B. am Ende des Videos False ist, und das frame1 nicht an den Algorithmus übergeben wird.
In den nächsten Schritten werden die gewünschten Operationen am Videobild frame durchgeführt, wie in den vorherigen Abschnitten beschrieben, und schließlich wird jedes Bild mit der Funktion cv2.imshow() angezeigt ( Abbildung 15). Zu diesem Zweck wird der zuvor kodierte Algorithmus ausgeschnitten und in die VideoCapture-Schleife eingefügt, und die vorherige statische Bildeingabe für die Funktionen canny(), average_slope_intercept() und display_lines() wird durch das Videobild frame ersetzt, wie im endgültigen Code unten gezeigt.
Der Parameter der Funktion waitKey() wird ebenfalls von $0$ auf $1$ Millisekunde geändert, damit das Programm $1$ zwischen den einzelnen Bildern wartet. Denn wenn der Wert $0$ ist, dann wartet das Programm unendlich lange zwischen den einzelnen Bildern im Video (wird eingefroren). Damit das Ausgabevideo, d. h. die while-Schleife, beim Drücken einer Taste, in diesem Fall q, geschlossen wird, weil sie sonst nicht geschlossen wird, bis sie die gesamte Dauer des Videos durchlaufen hat, wird dem Code innerhalb einer if -Anweisung die Funktion waitKey() hinzugefügt.
Die Funktion waitKey() gibt einen $32$-Bit-Ganzzahlwert der gedrückten Taste zurück. Dieser Wert wird mit der numerischen Kodierung des Unicode-Zeichens q auf der Tastatur verglichen, das der Taste entspricht, die gedrückt werden muss, um die Schleife zu unterbrechen (break). Der ganzzahlige Wert des Unicode-Zeichens q wird mit der eingebauten Funktion ord() ermittelt. Die bitweise UND-Verknüpfung & 0xFF wird hinzugefügt, um den von waitKey() zurückgegebenen Integer-Wert effektiv zu maskieren.
In hexadezimaler Darstellung (Basis $16$) entspricht F dem Wert $1111$ im binären Zahlensystem. Python verwendet das Präfix 0x für numerische Konstanten in hexadezimaler Darstellung. 0xFF ist also $11111111$ im Binärsystem, was dem Dezimalwert $255$ entspricht. Somit ist 0xFF ein Identitätselement für die bitweise UND-Verknüpfung. Wenn also der Dezimalwert der gedrückten Taste größer als $255$ ist, d.h. seine binäre Darstellung länger als $8$-Bits ist, werden nur die letzten $8$-Bits aus dem von waitKey() zurückgegebenen Wert genommen und mit dem Integer-Wert des Unicode-Zeichens q verglichen. Mit anderen Worten: Wenn dieser zurückgegebene Wert kleiner als $255$ ist, wird er nicht verändert. Andernfalls werden die letzten $8$-Bits des zurückgegebenen Wertes übernommen. Dies geschieht, um die plattformübergreifende Kompatibilität beim Vergleich zu gewährleisten.
Nachdem die Schleife unterbrochen wurde, wird die Videodatei durch den Aufruf von cap.release() geschlossen und alle Fenster, die während der Ausführung dieses Programms erstellt wurden, werden durch den Aufruf von cv2.destroyAllWindows() gelöscht.
import cv2
import numpy as np
def make_coordinates(image, line_parameters):
slope, y_intercept = line_parameters
y1 = image.shape[0]
y2 = int(y1*(3/5))
x1 = int((y1 - y_intercept)/slope)
x2 = int((y2 - y_intercept)/slope)
return np.array([x1, y1, x2, y2])
global_left_fit_average = []
global_right_fit_average = []
def average_slope_intercept(image, lines):
left_fit = []
right_fit = []
global global_left_fit_average
global global_right_fit_average
if lines is not None:
for line in lines:
x1, y1, x2, y2 = line.reshape(4)
parameters = np.polyfit((x1, x2), (y1, y2), 1)
slope = parameters[0]
y_intercept = parameters[1]
if slope < 0:
left_fit.append((slope, y_intercept))
else:
right_fit.append((slope, y_intercept))
if (len(left_fit) == 0):
left_fit_average = global_left_fit_average
else:
left_fit_average = np.average(left_fit, axis=0)
global_left_fit_average = left_fit_average
# left_fit_average = np.average(left_fit, axis=0)
right_fit_average = np.average(right_fit, axis=0)
global_right_fit_average = right_fit_average
left_line = make_coordinates(image, left_fit_average)
right_line = make_coordinates(image, right_fit_average)
return np.array([left_line, right_line])
def canny(image):
gray_image = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)
blur_image = cv2.GaussianBlur(gray_image,(5,5),0)
canny_image = cv2.Canny(blur_image, 50, 150)
return canny_image
def display_lines(image, lines):
line_image = np.zeros_like(image)
if lines is not None:
for x1, y1, x2, y2 in lines:
cv2.line(line_image,(x1,y1),(x2,y2),(255,0,0),10)
return line_image
def region_of_interest(image):
height = image.shape[0]
polygons = np.array([
[[200,height],[1100,height],[550,250]]
])
mask = np.zeros_like(image)
cv2.fillPoly(mask, polygons, 255)
masked_image = cv2.bitwise_and(image,mask)
return masked_image
# image1 = cv2.imread('test_image.jpg')
# lane_image = np.copy(image1)
# canny_image = canny(lane_image)
# cropped_image = region_of_interest(canny_image)
# linesP = cv2.HoughLinesP(cropped_image, 2, np.pi / 180, 100, np.array([]), minLineLength=40, maxLineGap=5)
# averaged_lines = average_slope_intercept(lane_image, linesP)
# line_image = display_lines(lane_image, averaged_lines)
# blended_image = cv2.addWeighted(lane_image, 0.8,line_image,1, 1)
# cv2.imshow("result", blended_image)
# cv2.waitKey(0)
cap = cv2.VideoCapture("test2.mp4")
while(cap.isOpened()):
success, frame1 = cap.read()
if success == False:
break
frame=frame1
canny_image = canny(frame)
cropped_image = region_of_interest(canny_image)
linesP = cv2.HoughLinesP(cropped_image, 2, np.pi / 180, 100, np.array([]), minLineLength=40, maxLineGap=5)
averaged_lines = average_slope_intercept(frame, linesP)
line_image = display_lines(frame, averaged_lines)
blended_image = cv2.addWeighted(frame, 0.8,line_image,1, 1)
cv2.imshow("result", blended_image)
if cv2.waitKey(1) & 0xFF == ord('q'):
break
cap.release()
cv2.destroyAllWindows()
