Künstliche Neuronale Netze und ihre Anwendung auf die industrielle Fehlerdiagnose von Pleuelstangen in Kompressoren: Einführung und Anwendungen

Erstellung neuronaler Netze mit MATLAB und Anwendung zur Lösung technischer Probleme wie Mustererkennung zur korrekten Sortierung von Paketen und Klassifizierung zur Fehlerdiagnose von Kompressorpleueln.

Neuronenmodell und Übertragungsfunktionen

1. Neuronenmodell

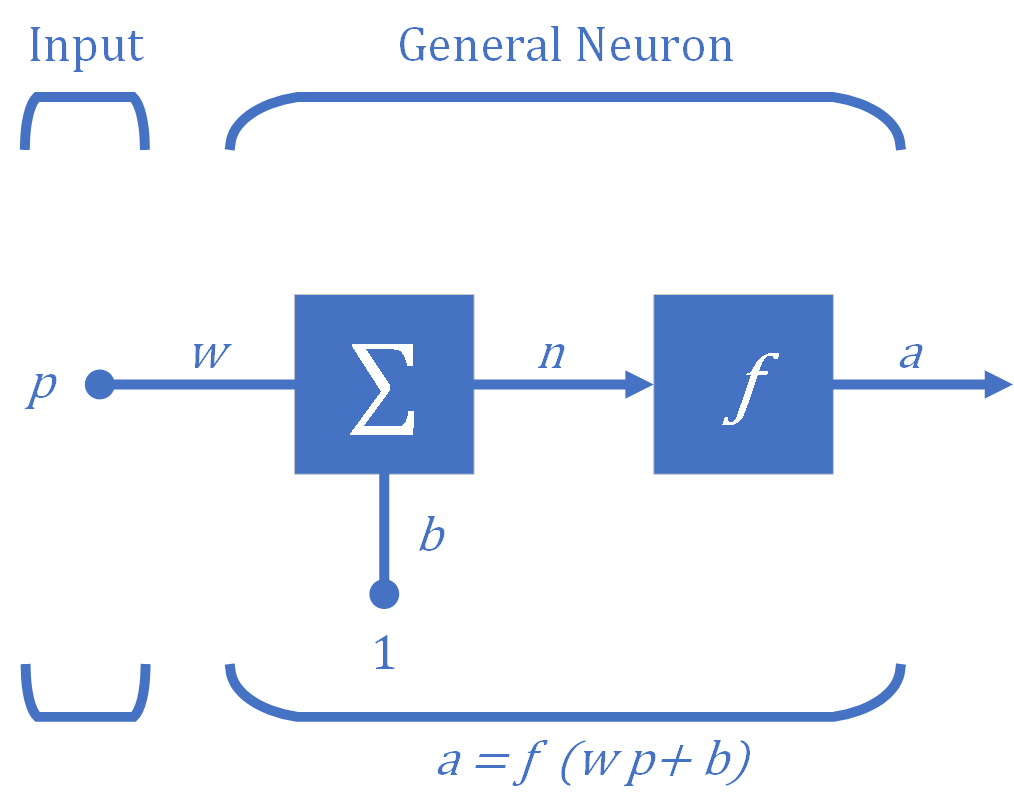
Der grundlegende Baustein für neuronale Netze ist das in Abbildung 1 dargestellte Neuron mit einem Eingang. In einem Neuron gibt es drei Funktionsabläufe.

• Zunächst wird die skalare Eingabe $p$ mit dem skalaren Gewicht $w$ multipliziert, um das Skalarprodukt $wp$ zu bilden. Dieser Vorgang wird als Gewichtsfunktion bezeichnet.
• Zweitens wird die gewichtete Eingabe $wp$ mit der skalaren Bias $b$ (auch "Offset" genannt) addiert, die wie eine Gewichtung ist, aber mit einer konstanten Eingabe von $1$, um die Nettoeingabe $n$ zu bilden. Dieser Vorgang wird als Nettoeingangsfunktion bezeichnet.
• Schließlich wird die Nettoeingabe $n$ durch die Übertragungsfunktion $f$ (auch "Aktivierungsfunktion" genannt) geleitet, die die skalare Ausgabe $a$ erzeugt. Dieser Vorgang wird als Übertragungsfunktion bezeichnet. Ohne die Angabe der Übertragungsfunktion kann die Ausgabe des Neurons nicht bestimmt werden.

2. Übertragungsfunktionen

Es gibt zahlreiche gebräuchliche Aktivierungsfunktionen. Im folgenden Code werden vier Aktivierungsfunktionen für eine Nettoeingabe $n$ berechnet und gezeichnet:

1. Hyperbolisch-tangentiale sigmoide Übertragungsfunktion: $$a=f\left(n\right)=\mathrm{tansig}\left(n\right)=\frac{2}{1+e^{-2n} }-1$$
2. Exponentiale Übertragungsfunktion: $$a=f\left(n\right)=\frac{2}{1+e^{-n} }-1$$
3. Hard-Limit-Übertragungsfunktion: $$a=f\left(n\right)=\mathrm{hardlim}\left(n\right)=\left\lbrace \begin{array}{ll} 1 & \mathrm{if}\;n\ge 0\\ 0 & \mathrm{otherwise} \end{array}\right.$$
4. Lineare Übertragungsfunktion: $$a=f\left(n\right)=\mathrm{purelin}\left(n\right)=n$$

wobei die Nettoeingabe $n=\mathbf{Wp}+b=2p+3$ ist, wenn die Gewichtung $w$ der einzelnen Eingabe $p$ gleich $2$ und der Bias $b$ gleich $3$ ist.

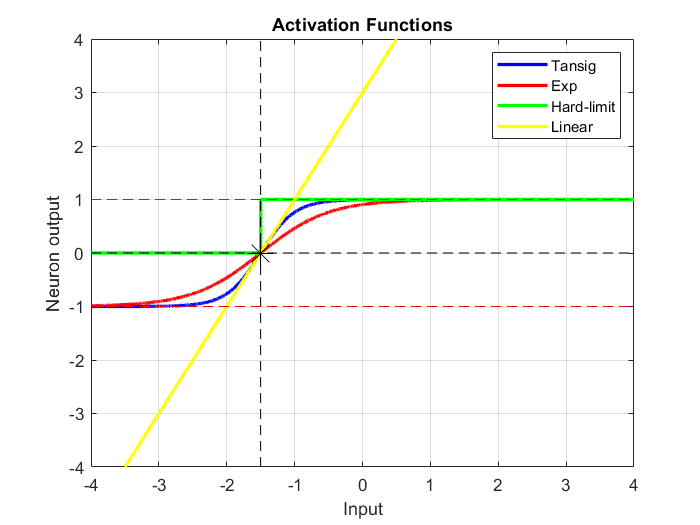
Die exponentielle Übertragungsfunktion ist normalisiert und von Null abgehoben, so dass die Ausgabe zwischen $-1$ und $1$ liegt.

Die hyperbolische Tangens-Sigmoid-Übertragungsfunktion (tansig oder tanh) und die Exponentialübertragungsfunktion sind sehr ähnlich. Sie setzen der Ausgabe Grenzen. In diesem Fall innerhalb des Bereichs $-3 ≤ n < 1$, in dem sie die Funktion der Eingabe zurückgeben. Außerhalb dieser Grenzen geben sie $-1$ oder $1$ zurück.

Die hard-limit Übertragungsfunktion (hardlim) gibt $0$ zurück, wenn der Wert kleiner als ein Schwellenwert ist, und $1$, wenn er größer oder gleich dem Schwellenwert ist, hier $-1,5$.

Die lineare Übertragungsfunktion berechnet einfach die Ausgabe des Neurons, indem sie einfach den Wert $n$ zurückgibt, der ihr übergeben wurde.

Der folgende Code berechnet diese vier Aktivierungsfunktionen für eine Nettoeingabe $n$ und stellt sie dar:

Die zentrale Idee neuronaler Netze besteht darin, die einstellbaren skalaren Parameter $w$ und $b$ des Neurons so anzupassen, dass das Netz ein gewünschtes oder interessantes Verhalten zeigt. Dieses Verfahren wird als Perceptron-Lernregel oder Trainingsalgorithmus bezeichnet.

Mehrfacheingabe-Neuron

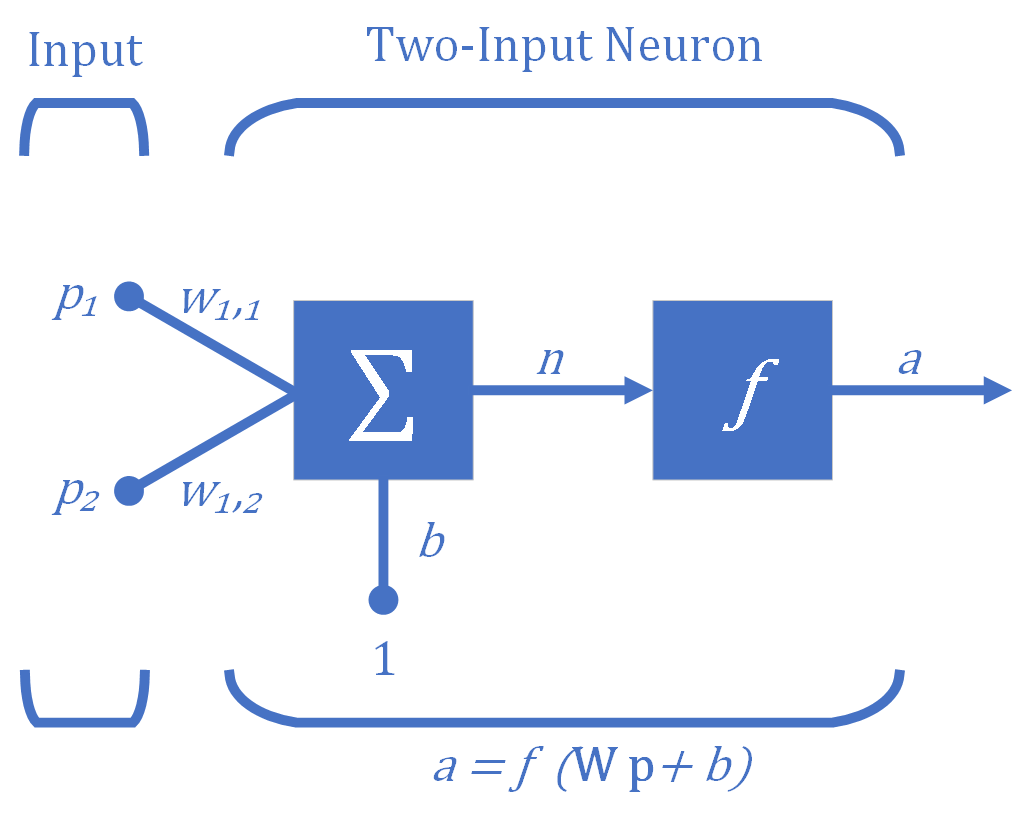
Das einfache Neuron kann erweitert werden, um Eingaben zu verarbeiten, die Vektoren sind. Ein Neuron mit einem einzigen Zwei-Elemente-Eingangsvektor $(R=2)$ ist in Abbildung 3 dargestellt, wobei die einzelnen Eingangselemente $p_1$ und $p_2$ mit den Gewichten $w_{1,1}$ und $w_{1,2}$ des Neurons (hier gibt es ein Neuron) multipliziert und die gewichteten Werte der summierenden Verzweigung zugeführt werden. Ihre Summe ist einfach $\textbf{Wp}$, das Punktprodukt, das einfach die Summe der komponentenweisen Produkte der Vektorkomponenten der (einzeiligen) Matrix $\textbf{W}$ und des Vektors $\textbf{p}$ ist. Das Neuron hat einen Bias (Offset) $b$, der mit den gewichteten Eingängen summiert wird, um die Nettoeingabe $n$ zu bilden. Die Nettoeingabe $n$ ist das Argument der Übertragungsfunktion $f$.

Eine Entscheidungsgrenze wird durch die Eingangsvektoren bestimmt, für die die Nettoeingabe $n$ gleich Null ist.

Damit wird eine Grenze im Eingaberaum (Merkmalsraum) definiert, eine lineare Trennlinie, die den Eingaberaum in zwei Teile unterteilt. Ein Eingaberaum umfasst alle möglichen Wertemengen für die Eingabe. Wenn das innere Produkt der Gewichtsmatrix $\textbf{W}$ (in diesem Fall ein einzeiliger Vektor) mit dem Eingabevektor $\textbf{p}$ größer oder gleich $-b$ ist, ist die Ausgabe positiv $(n>1)$, andernfalls ist die Ausgabe negativ $(n<1)$. Abbildung 4 veranschaulicht dies für den Fall, dass $b = -3$. Die blaue Linie in der Abbildung, die lineare Trennlinie, wird in drei Dimensionen als Ebene oder Hyperebene bezeichnet und stellt alle Punkte dar, für die die Nettoeingabe $n$ gleich Null ist und somit im Eingabe-Ausgabe-Raum das Ergebnis der Übertragungsfunktion $f$, in diesem Fall die hyperbolische Tangens-Sigmoid-Übertragungsfunktion, ebenfalls Null ist. Der schattierte Bereich enthält alle Eingangsvektoren, für die der Ausgang des Netzes näher oder gleich $1$ ist. Für alle anderen Eingangsvektoren ist der Ausgang näher oder gleich $-1$ (der nicht schattierte Bereich).

Im Grunde gibt es eine unendliche Menge von Gleichungen, die alle dasselbe Trennzeichen darstellen, da die Multiplikation beider Seiten der Gleichung mit einer beliebigen Zahl die Gleichheit nicht beeinträchtigt.

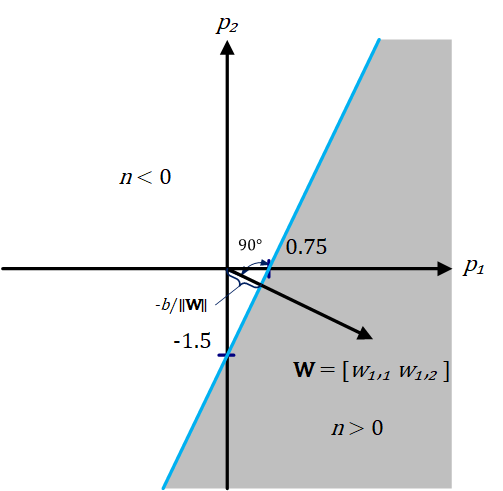
Die Entscheidungsgrenze, eine Hyperebene, wird immer orthogonal zur Gewichtsmatrix sein, und die Position der Grenze kann durch Änderung von $b$ verschoben werden. Zur Verdeutlichung: Nach der Definition der Orthogonalität in der Mathematik sind zwei Vektoren im euklidischen Raum dann und nur dann orthogonal, wenn ihr Punktprodukt gleich Null ist, d. h. wenn sie einen Winkel von $90°$ bilden. Aus der Definition der Hyperebene in der Geometrie geht hervor, dass eine Hyperebene ein Unterraum ist, dessen Dimension um eins kleiner ist als die des ihn umgebenden Raums. In einem zweidimensionalen Raum wäre eine Hyperebene also eine Linie.

Für einen $n$-dimensionalen Raum ist eine Ebene durch die Gleichung definiert:

wobei $\textbf{w}$ und $\textbf{p}$ jeweils Vektoren der Länge $n$ sind. $\textbf{w}$ ist ein Vektor orthogonal zur Ebene, die den Vektor $\textbf{p}$ enthält, und $b$ ist proportional zum senkrechten Abstand vom Ursprung zur Ebene (der Entscheidungsgrenze). Die Proportionalitätskonstante ist das Negativ des Betrags des Normalenvektors.

Zusammenfassend lässt sich sagen, dass das Ziel des Lernens in einem Perzeptron mit einem Ausgang im Allgemeinen darin besteht, die trennende Hyperebene (d.h. die lineare Entscheidungsgrenze), die einen $n$-dimensionalen “Eingaberaum” teilt, anzupassen, wobei $n$ die Anzahl der Nettoeingaben ist, indem die Gewichte und der Bias so lange verändert werden, bis sich alle Eingabevektoren mit dem Zielwert $1$ auf einer Seite der Hyperebene und alle Eingabevektoren mit dem Zielwert $0$ oder $-1$, je nach Aktivierungsfunktion, auf der anderen Seite der Hyperebene befinden. In einem Nework mit mehreren Neuronen ist $\textbf{W}$ eine Matrix, die aus einer Reihe von Zeilenvektoren besteht, von denen jeder in einer Gleichung ähnlich der obigen verwendet wird. Für jede Zeile von $\textbf{W}$ gibt es eine Begrenzung.

Die Schlüsseleigenschaft des Ein-Neuronen-Perzeptrons ist daher, dass es Eingangsvektoren in zwei Kategorien trennen kann. Da die Grenze linear ist, kann das einschichtige Perzeptron nur zur Klassifizierung von Eingaben verwendet werden, die linear trennbar sind (durch eine lineare Grenze getrennt werden können).

Zur Definition eines Netzes sind die folgenden Problemspezifikationen hilfreich:

1. Anzahl der Netzeingaben = Anzahl der Problemeingaben
2. Anzahl der Neuronen in der Ausgabeschicht = Anzahl der Problemausgaben
3. Die Wahl der Übertragungsfunktion der Ausgabeschicht wird zumindest teilweise durch die Problemstellung der Ausgänge bestimmt

Problembeschreibung

Berechnung der Ausgabe eines einfachen Neurons.

Schritte

1. Festlegung der Neuronenparameter
2. Festlegung des Eingangsvektors
3. Berechnung der Neuronenausgabe
4. Aufzeichnung der Neuronenausgabe über den Bereich der Eingaben

1. Festlegung der Neuronenparameter

Als Beispiel für ein Zwei-Eingabe-Perzeptron mit einem Neuron, wie in Abbildung 2 oben dargestellt, werden die folgenden Werte für die Gewichte und den Bias zugewiesen:

Im Falle eines einzelnen Neurons ist die skalare Nettoeingabe $n$ für die Übertragungsfunktion $f$, die die skalare Neuronenausgabe $a$ erzeugt, gegeben durch:

• $$ n=\ \mathit{\mathbf{p}}*\ {\mathit{\mathbf{W}}}^T +b $$
• $$ ={\left[\begin{array}{cc} p_1 & p_2 \end{array}\right]}\cdot {\left[\begin{array}{cc} 4 & -2 \end{array}\right]^{T}} -3 $$
• $$ =4p_1 -2p_2 -3 $$

2. Festlegung des Eingangsvektors

3. Berechnung der Neuronenausgabe

Der Ausgang dieses Netzes wird durch eine Übertragungsfunktion bestimmt, zum Beispiel die hyperbolische Tangens-Sigmoid-Übertragungsfunktion tansig.

4. Aufzeichnung der Neuronenausgabe über den Bereich der Eingaben

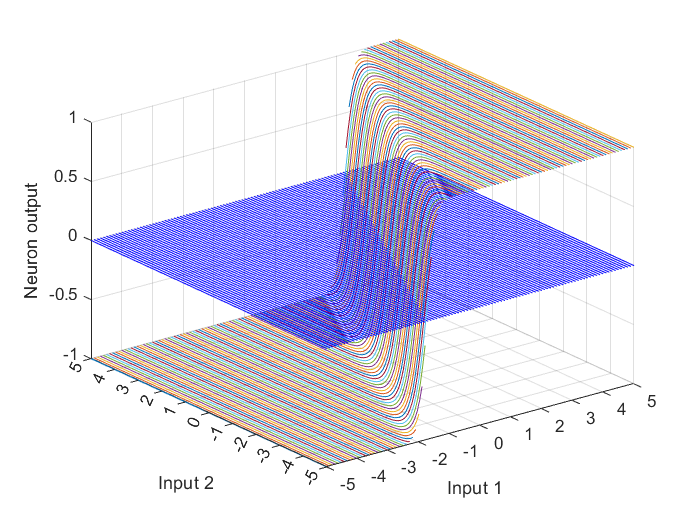
Das oben beschriebene Neuron mit einer Vektoreingabe könnte im Eingabe-Ausgabe-Raum veranschaulicht werden, indem die Netzwerkausgabe über den Bereich der Eingabewerte für $p_1$ und $p_2$ grafisch dargestellt wird, wie in Abbildung 5 gezeigt. Zu diesem Zweck wird hier die MATLAB-Funktion meshgrid verwendet, um zwei Matrizen $p_1$ und $p_2$ mit einer Größe von jeweils $101 \times 101$ zu erstellen. Die Funktion meshgrid gibt 2-D-Gitterkoordinaten zurück, die auf den Koordinaten basieren, die in dem zugewiesenen Vektor zwischen den Klammern enthalten sind. $p_1$ ist eine Matrix, bei der jede Zeile eine Kopie des zugeordneten Vektors ist, und $p_2$ ist eine Matrix, bei der jede Spalte eine Kopie des zugeordneten Vektors ist.

Um den Ausgang des Neurons zu finden, wird die Funktion mit den Eingangswerten ausgewertet, die sich in diesem Fall aus der Gleichung $4p_1 -2p_2 -3$ ergeben.

Die Art der Ein- und Ausgänge hängt von der Funktion ab, in diesem Fall von der Hyperbeltangens-Sigmoid-Transferfunktion tansig, die eine Matrix von Nettoeingabe-Spaltenvektoren annimmt und eine Spaltenvektor-Matrix derselben Größe zurückgibt, die aus den Elementen des Eingabe-Spaltenvektors besteht, wobei jedes Element aus dem Intervall $[-inf \quad inf]$ in das Intervall $[-1 \quad 1]$ mit einer “S-förmigen” Kurve gequetscht wird.

Um die Ein- und Ausgänge mit der MATLAB-Funktion plot3 in einem 3-D-Diagramm darzustellen, müssen die Ein- und Ausgabematrizen mindestens eine gleich große Dimension haben. In diesem Fall haben die Eingabe- und Ausgabematrizen jedoch keine gleich große Dimension. Daher wird die Funktion reshape verwendet, um den Ausgabespaltenvektor a umzuformen und ein umgestaltetes Array a mit der folgenden Größe zurückzugeben: $length\left(p_{1} \right) \times length\left(p_{2} \right)$.

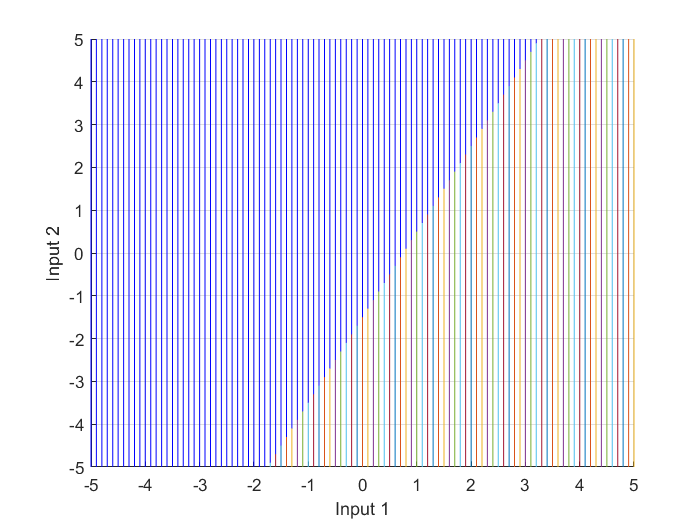
The next lines of code shows the top-view of the input-output space plot, Figure 6, which is the input-space, where the intersection of the decision boundary with the transfer function curves is a line, similar to the linear separator previously illustrated in Figure 4.

Die nächsten Codezeilen zeigen die Draufsicht auf den Eingabe-Ausgabe-Raum, Abbildung 6, d. h. den Eingaberaum, in dem der Schnittpunkt der Entscheidungsgrenze mit den Übertragungsfunktionskurven eine Linie ist, ähnlich der linearen Trennlinie, die zuvor in Abbildung 4 dargestellt wurde.

Mehrfach-Neuronen-Perzeptron

Wie bereits erwähnt, hat jedes Neuron eine einzige Entscheidungsgrenze. Ein Perzeptron mit nur einem Neuron kann Eingabevektoren in zwei Kategorien klassifizieren, da seine Ausgabe entweder $0$ oder $1$ sein kann. Ein Perzeptron mit mehreren Neuronen kann die Eingaben in viele Kategorien einteilen. Jede Kategorie wird durch einen anderen Ausgabevektor repräsentiert. Da jedes Element des Ausgabevektors entweder $0$ oder $1$ sein kann, gibt es insgesamt $2^S$ mögliche Kategorien, wobei $S$ die Anzahl der Neuronen ist. Bei einem Perzeptron mit mehreren Neuronen wird die Entscheidungsgrenze für jedes Neuron $i$ wie folgt definiert:

Perzeptron-Lernregel

Unter Lernregel versteht man ein Verfahren (einen Algorithmus) zur Änderung der Gewichte und Bias eines Netzes. (Dieses Verfahren wird auch als Trainingsalgorithmus bezeichnet). Der Zweck der Lernregel besteht darin, das Netz auf eine bestimmte Aufgabe zu trainieren, z. B. auf die Lösung eines Klassifizierungsproblems. Es gibt viele Arten von Trainingsalgorithmen (Lernregeln) für neuronale Netze. Sie lassen sich in drei große Kategorien einteilen: überwachtes Lernen, unüberwachtes Lernen und verstärkendes (oder abgestuftes) Lernen.

Beim überwachten Lernen wird die Lernregel mit einer Reihe von Beispielen (der Trainingsmenge) für das richtige Verhalten des Netzes (Eingaben und deren Zielausgaben) versorgt:

wobei $\textbf{p}_q$ eine Eingabe für das Netz und $\textbf{t}_q$ die entsprechende korrekte (Ziel-)Ausgabe ist. Während die Eingaben auf das Netz angewendet werden, werden die Netzausgaben mit den Zielwerten verglichen. Die Lernregel wird dann verwendet, um die Gewichte und Bias des Netzes anzupassen, um die Netzausgänge näher an die Ziele zu bringen.

Verstärkungslernen ähnelt dem überwachten Lernen, mit dem Unterschied, dass der Algorithmus nicht für jede Netzwerkeingabe die richtige Ausgabe erhält, sondern nur eine Bewertung. Die Bewertung (oder Punktzahl) ist ein Maß für die Leistung des Netzes über eine Reihe von Eingaben.

Beim unüberwachten Lernen werden die Gewichte und Bias nur in Reaktion auf die Eingaben des Netzes geändert. Es sind keine Zielausgaben verfügbar.

Um mit dem Training zu beginnen und die Lernregeln zu erstellen, werden einige Anfangswerte für die Netzwerkparameter (Gewichte und Bias) zugewiesen. Dann werden dem Netz die Eingangsvektoren nacheinander vorgelegt. Jedes Mal, wenn das Netz nicht den richtigen Wert liefert (die Zielausgabe, die mit der Eingabe verbunden ist), wird der Gewichtsvektor so verändert, dass er mehr in Richtung des Eingabevektors zeigt. Wenn das Netz den richtigen Wert liefert, muss nichts geändert werden. Auf diese Weise wird ein einziger Ausdruck gefunden, der einer einheitlichen Lernregel ähnelt. Hierfür wird zunächst eine neue Variable definiert, der Perzeptron-Fehler $e$:

wobei $e$ der falsche Ausgabewert (auch Fehler genannt) ist. Er ist gleich $0$, wenn das Netz die richtige Ausgabe $(t=a)$ liefert. Auf diese Weise lautet die einheitliche Lernregel für Perzeptronen mit mehreren Neuronen in Matrixschreibweise:

und

Obwohl die Perzeptron-Lernregel einfach ist, ist sie sehr leistungsfähig. Sie wird immer zu Gewichten konvergieren, die die gewünschte Klassifizierung erreichen (vorausgesetzt, dass solche Gewichte existieren).

Ein anschauliches Beispiel

Das folgende Beispiel soll zeigen, wie die in den vorangegangenen Abschnitten beschriebenen Architekturen zur Lösung eines einfachen praktischen Problems - eines Mustererkennungsproblems - verwendet werden können, indem drei verschiedene neuronale Netzarchitekturen eingesetzt werden: ein einschichtiges Perzeptron (Feedforward-Netz) mit einer symmetrischen Hard-Limit-Übertragungsfunktion hardlims, ein Hamming-Netz (kompetitives Netz) und ein Hopfield-Netz (rekurrentes assoziatives Speichernetz).

Problembeschreibung

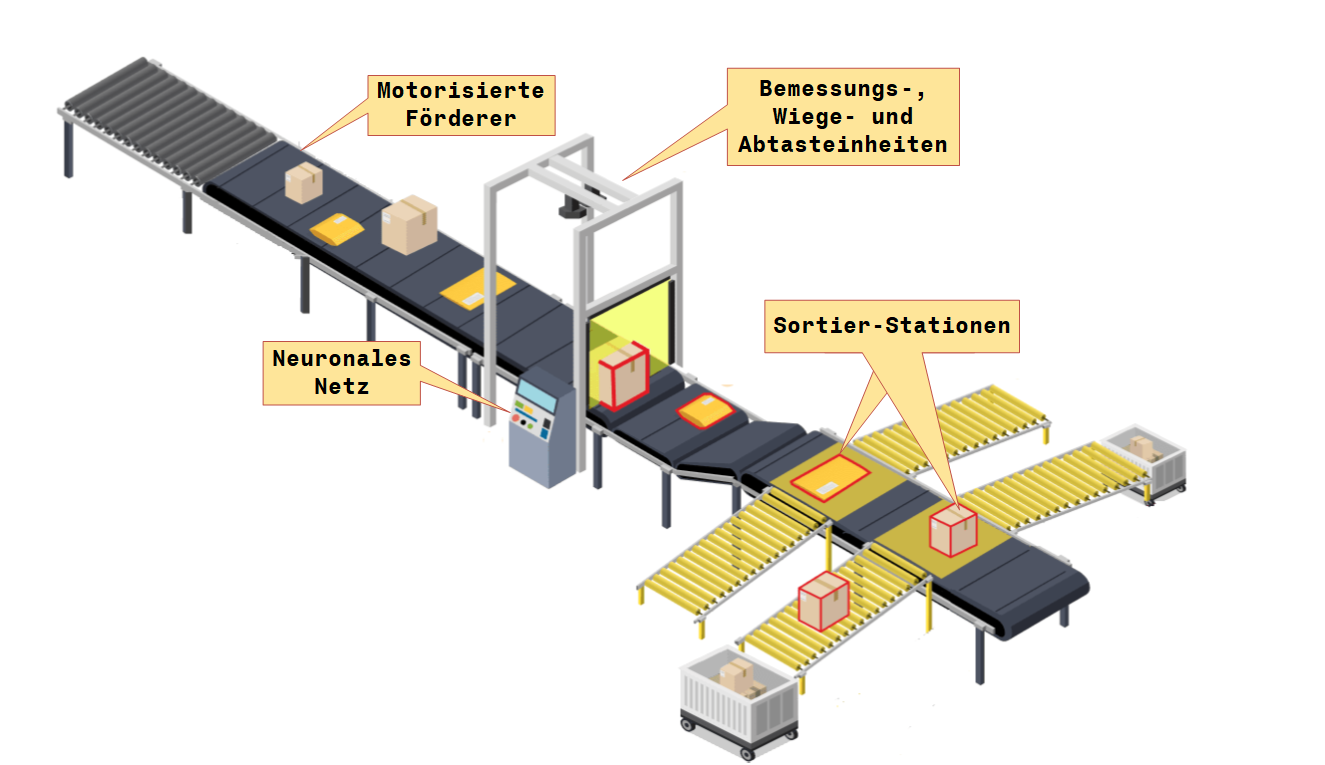
Eine zentrale Bearbeitungsstation verfügt über eine Paketsortiermaschine, die mit Hilfe von Scan-, Volumen- und Wiegetechniken Pakete identifizieren und genau profilieren kann, wie in Abbildung 7 dargestellt. Wenn die Pakete eine zentrale Bearbeitungsstation erreichen, können verschiedene Arten von Paketen miteinander vermischt sein. Ziel ist es, die Pakete nach ihrer Art zu sortieren. Es gibt ein Förderband, auf das die Pakete geladen werden. Dieses Förderband durchläuft eine Reihe von Sensoren, die drei Eigenschaften des Pakets messen: Größe, Form und Gewicht. Es wird angenommen, dass diese Sensoren zwei Werte $1$ und $-1$ ausgeben werden. Der Größensensor gibt einen Wert von $1$ aus, wenn es sich um ein mittelgroßes Paket handelt, und einen Wert von $-1$, wenn es sich um ein Paket handelt. Der Formsensor gibt einen Wert von $1$ aus, wenn das Paket ungefähr rund ist, und einen Wert von $-1$, wenn es eher rechteckig ist. Der Gewichtssensor gibt eine $1$ aus, wenn das Paket mehr als $10$ Kilogramm wiegt, und eine $-1$, wenn das Paket gleich oder weniger als $10$ Kilogramm wiegt.

Die drei Sensorausgänge werden dann in ein neuronales Netz eingegeben. Der Zweck des Netzes ist es, zu entscheiden, welche Art von Paket sich auf dem Förderband befindet, damit das Paket in die richtige Richtung geleitet werden kann. Um das Problem noch weiter zu vereinfachen, wird angenommen, dass sich nur zwei Arten von Paketen auf dem Förderband befinden: Typ A (mittelgroß, rechteckig, schwerer als 10 Kilogramm) und Typ B (Paket, rechteckig, gleich oder weniger als 10 Kilogramm).

Ziele

1. Entwurf eines Perzeptrons (Feedforward-Netzwerk) zur Erkennung von Mustern
2. Bestimmung und Skizzierung einer Entscheidungsgrenze für das Perzeptron-Netz, das diese prototypischen Muster erkennen soll.
3. Bestimmung von Gewichten und Bias, die zu dieser Entscheidungsgrenze führen
4. Entwurf eines Hamming-Netzes (Wettbewerbsnetz) zur Erkennung dieser Muster
5. Entwurf eines Hopfield-Netzes (rekurrentes assoziatives Speichernetz) zur Erkennung dieser Muster

Lösung

1. Entwurf eines Perzeptrons (Feedforward-Netzwerk) zur Erkennung von Mustern

Da jedes Paket die Sensoren durchläuft, kann es durch einen dreidimensionalen Vektor dargestellt werden. Das erste Element des Vektors steht für die Größe, das zweite Element für die Form und das dritte Element für das Gewicht:

Ein Prototyp vom Typ A würde also durch den Vektor dargestellt:

und ein Typ B-Prototyp würde durch den Vektor dargestellt werden:

Das neuronale Netz erhält für jedes Paket auf dem Förderband einen dreidimensionalen Eingangsvektor und muss entscheiden, ob das Paket vom Typ A $(\textbf{p}_1)$ oder vom Typ B $(\textbf{p}_2)$ ist.

Da es nur zwei Kategorien gibt, können wir ein Perzeptron mit einem einzigen Neuron verwenden. Die Vektoreingaben sind dreidimensional $(R=3)$, daher lautet die Gleichung des Perzeptrons:

2. Bestimmung und Skizzierung einer Entscheidungsgrenze

Der Bias und die Elemente der Gewichtsmatrix werden so gewählt, dass das Perzeptron in der Lage ist, zwischen Parzellen des Typs A und des Typs B zu unterscheiden. Das Perzeptron wird beispielsweise so konfiguriert, dass die Ausgabe $1$ beträgt, wenn eine Parzelle des Typs A eingegeben wird, und $-1$, wenn eine Parzelle des Typs B eingegeben wird. Unter Verwendung des in Abbildung 4 dargestellten Konzepts gibt es eine lineare Grenze, die Parzellen vom Typ A und Parzellen vom Typ B trennen kann. Die beiden Prototyp-Vektoren sind in den nächsten beiden Diagrammen, Abbildung 8 und Abbildung 9, dargestellt. Die Abbildungen zeigen die lineare Grenze, die diese beiden Vektoren symmetrisch trennt, nämlich die Ebene $p_2, p_3$.

In MATLAB:

Der MATLAB-Code für die benutzerdefinierte Funktion viewProtypeVect, die im vorherigen Code zur Darstellung beider Ansichten verwendet wurde, ist wie folgt:

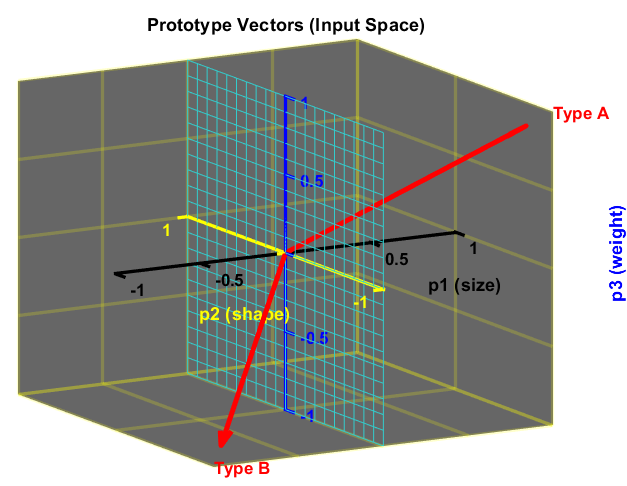
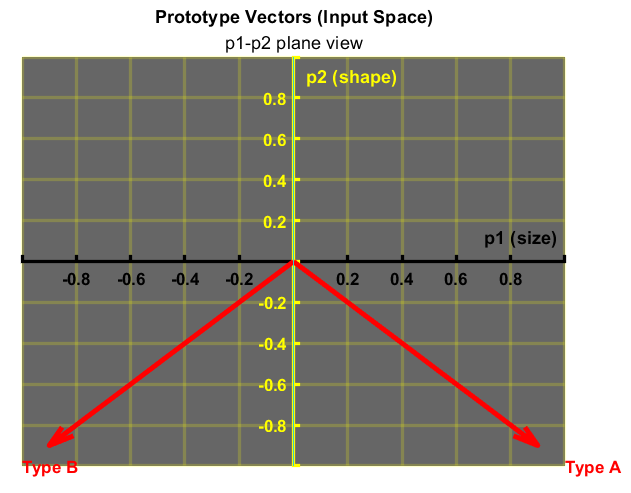
3. Bestimmung von Gewichten und Bias, die zu dieser Entscheidungsgrenze führen

Die Ebene $p_2, p_3$, die Entscheidungsgrenze, kann durch die folgende Gleichung beschrieben werden:

oder

Daher lauten die Gewichtungsmatrix und der Bias:

Die Gewichtsmatrix ist orthogonal zur Entscheidungsgrenze und zeigt in Richtung der Region, die das Prototypmuster Typ A enthält, für das das Perzeptron eine Ausgabe von 1 erzeugen soll. Der Bias ist 0, da die Entscheidungsgrenze durch den Ursprung verläuft.

Die Prüfung der Funktionsweise des Perzeptron-Musterklassifikators zeigt, dass er Typ A und Typ B korrekt klassifiziert:

• Pakete des Typs A (mittelgroß, rechteckig, schwerer als 10 Kilogramm):

• Paket des Typs B (Paket, rechteckig, bis 10 Kilogramm):

Wenn jedoch ein nicht so perfektes Paket des Typs B in den Klassifikator eingegeben wird, wird beispielsweise ein Paket des Typs B, das eher rund ist, durch die Sensoren geleitet. Der Eingabevektor würde dann sein:

Die Antwort des Netzes wäre vom Typ B:

In der Tat wird jeder Eingangsvektor, der näher am Prototyp-Vektor vom Typ B als am Prototyp-Vektor vom Typ A (im euklidischen Abstand) liegt, als Typ B eingestuft (und umgekehrt).

In MATLAB könnte dieser Perzeptron-Entwurf folgendermaßen kodiert werden:

was zu der folgenden Ausgabe führt:

4. Hamming-Netzwerk

Das Hamming-Netz wurde ausdrücklich zur Lösung von binären Mustererkennungsproblemen entwickelt, bei denen jedes Element des Eingangsvektors nur zwei mögliche Werte $1$ oder $0$ hat, sowie zur Lösung eines bipolaren Mustererkennungsproblems, wie in diesem Beispiel, bei dem die Elemente des Eingangsvektors die Werte $1$ oder $-1$ haben. Das Hamming-Netzwerk ist ein Clusternetzwerk. Es basiert auf der Verwendung von festen Prototyp-Vektoren (Exemplaren) und einer rekurrenten Schicht.

Das Hamming-Netz besteht aus zwei Arten von Schichten:

• Feedforward-Schicht, eine Korrelationsschicht, bei der alle Neuronen mit allen Eingängen des Netzes verbunden sind;
• rekurrente Schicht (Backpropagation), eine kompetitive Schicht, bei der der Ausgang jedes Neurons mit genau einem Neuron der Eingangsschicht verbunden ist.

Einige Quellen nennen die Feedforward-Schicht als Hamming-Netz, das misst, wie sehr der Eingangsvektor dem Gewichtsvektor jedes Neurons ähnelt, und die rekurrente oder Backpropagation-Schicht wie MAXNET; ein neuronales Netz, das auf Wettbewerb basiert und als Teilnetz verwendet werden kann, um das Neuron auszuwählen, dessen Aktivierung am größten ist.

Im Hamming-Netz ist die Anzahl der Neuronen $S$ in der ersten (Feedforward-) Schicht gleich der Anzahl der Neuronen in der zweiten (Feedback-) Schicht und entspricht der Anzahl der Prototypmuster (in diesem Beispiel $S = 2$). Rekurrente Netze können ein zeitliches Verhalten aufweisen.

Bei jeder Eingabe ermittelt die Feedforward-Schicht über das Punktprodukt den Abstand zwischen dem Gewichtsvektor jedes Neurons, also dem Prototypvektor, und dem Eingabevektor, während die rekurrente Schicht, d.h. MAXNET, das Neuron mit dem größten Punktprodukt auswählt. Auf diese Weise wählt das gesamte Netz das Neuron, d.h. den Prototypvektor, dessen Gewichtsvektor dem Eingangsvektor am nächsten liegt, d.h. den Gewinner.

Auf diese Weise besteht das Ziel des Hamming-Netzes darin, zu entscheiden, welcher Prototyp-Vektor dem Eingangsvektor am ähnlichsten ist. Diese Entscheidung wird durch den Ausgang der rekurrenten Schicht angezeigt. In der rekurrenten Schicht gibt es ein Neuron für jedes Prototypmuster. Wenn die rekurrente Schicht konvergiert, gibt es nur noch ein Neuron mit einer Ausgabe ungleich Null. Dieses Neuron zeigt das Prototypmuster an, das dem Eingabevektor am ähnlichsten ist.

Die Feedforward-Schicht führt eine Korrelation oder ein inneres Produkt zwischen jedem der Prototypmuster und dem Eingabemuster durch. Dazu werden die Zeilen der Gewichtsmatrix in der Feedforward-Schicht, die durch die Verbindungsmatrix ${\mathbf{W}}^1$ der Größe $S\times R$ (hier $2\times 3$) repräsentiert wird, auf die Prototypenmuster \(\textbf{p}_{\textbf{1}}\) und \(\textbf{p}_{\textbf{2}}\) gesetzt. $R$ ist die Anzahl der Elemente im Eingabevektor (hier $R = 3$).

Für dieses anschauliche Beispiel würde dies bedeuten:

Anmerkung: Die hochgestellten Zahlen geben die Nummer der Schicht an.

Die Feedforward-Schicht verwendet eine lineare Übertragungsfunktion, und jedes Element des Bias-Vektors ist gleich $R$. Der Bias-Vektor würde also sein:

Mit dieser Wahl für die Gewichtsmatrix und den Bias-Vektor ist die Ausgabe der Feedforward-Schicht gleich den Punktprodukten (auch innere Produkte genannt) jedes Prototypmusters mit der Eingabe, plus $R$.

Das liegt daran, dass bei zwei Vektoren gleicher Länge (Betrag oder Norm) ihr Punktprodukt am größten ist, wenn die Vektoren in dieselbe Richtung zeigen (der Kosinus des Winkels zwischen ihnen ist gleich $1$), und am kleinsten, wenn sie in entgegengesetzte Richtungen zeigen (der Kosinus des Winkels zwischen ihnen ist gleich $-1$). Um zu gewährleisten, dass die Ausgänge der Feedforward-Schicht niemals negativ sind, wird außerdem $R$ zum Punktprodukt addiert. Dies ist für das ordnungsgemäße Funktionieren der rekurrenten Schicht erforderlich.

Die Ausgabe ist hier eine $S\times 1$-Spaltenvektormatrix und kein Skalar, wie es bei dem Netz mit einem Neuron der Fall war.

Dieses Netz wird Hamming-Netz genannt, weil das Neuron in der Feedforward-Schicht mit der größten Ausgabe dem Prototypmuster entspricht, das dem Eingabemuster in der Hamming-Distanz am ähnlichsten ist. Die Hamming-Distanz ist definitionsgemäß der Abstand zwischen zwei binären (oder bipolaren) Vektoren gleicher Länge, der der Anzahl der Elemente zwischen den beiden Vektoren entspricht, die sich unterscheiden. Das Feedforward-Netz wählt das Prototypmuster (den Gewichtsvektor) aus, das eine minimale Hamming-Distanz ergibt (d. h. das Prototypmuster, das dem Eingabemuster in der Hamming-Distanz am ähnlichsten ist). Mit anderen Worten: Es wird gemessen, wie sehr der Eingangsvektor dem Gewichtsvektor jedes Neurons ähnelt.

Zum Beispiel ist der Hamming-Abstand zwischen den Vektoren \(\textbf{p}_{\textbf{1}} =\left[\matrix{ 1\cr -1\cr 1} \right]\) und \(\textbf{p} = \left[\matrix{ 1\cr 1\cr 1} \right]\) gleich $1$, da sie sich an einer Stelle unterscheiden. In ähnlicher Weise ist der Hamming-Abstand zwischen \(\textbf{p}_{\textbf{2}} = \left[\matrix{ -1\cr -1\cr -1} \right]\) und \(\textbf{p} = \left[\matrix{ 1\cr 1\cr 1} \right]\) gleich $3$, da sie sich an drei Stellen unterscheiden.

Die Ausgabe der Feedforward-Schicht wäre:

\(\text{a}^{1} = \left[ \left[\matrix{ 1 &-1& 1\cr -1 &-1 &-1} \right] \cdot \left[\matrix{1 \cr 1 \cr 1}\right]+ \left[\matrix{ 3\cr 3} \right] \right]\) \(= \left[\matrix{ 1\cr -3}\right] +\left[\matrix{ 3\cr 3}\right] = \left[\matrix{ 4\cr 0} \right]\)

könnte dies folgendermaßen geschrieben werden:

\(\text{a}^{1} = \left[\matrix{ 4\cr 0} \right] = \left [\matrix{ 2*(3-1)\cr 2*(3-3)} \right]\) \(= 2 * \left [\matrix{ 3-1\cr 3-3}\right] = 2 * \left [\matrix{ R-1\cr R-3} \right]\)

Die Ausgänge der Feedforward-Schicht sind somit gleich $2R$ minus der doppelten Hamming-Distanz zwischen den Prototypmustern und dem Eingabemuster.

Die rekurrente Schicht des Hamming-Netzes ist eine so genannte kompetitive Schicht. Die Neuronen in dieser Schicht werden mit den Ausgaben der Feedforward-Schicht initialisiert, die die Korrelation zwischen den Prototyp-Mustern und dem Eingangsvektor angeben. Dann treten die Neuronen gegeneinander an, um einen Gewinner zu ermitteln. Nach Abschluss des Wettbewerbs hat nur ein Neuron (der Gewinner) in der Gruppe eine Ausgabe ungleich Null. Diese extremste Form des Wettbewerbs zwischen einer Gruppe von Neuronen wird Winner-Take-All genannt. Das siegreiche Neuron gibt an, welche Kategorie von Eingaben dem Netzwerk präsentiert wurde.

Die rekurrente Schicht hat $S$ Neuronen, die vollständig miteinander verbunden sind. Jedes Neuron ist mit jedem anderen Neuron in der Schicht verbunden, auch mit sich selbst. Die von den Neuronen verwendete Übertragungsfunktion ist die poslin-Übertragungsfunktion, eine positiv-lineare Funktion, die für positive Werte linear und für negative Werte null ist.

Die Gewichte der rekurrenten Schicht sind symmetrisch, fest und werden durch folgende Formel angegeben:

wobei \(\epsilon\) eine vorgegebene positive Konstante ist. Sie muss positiv und kleiner als $1$ sein. Die diagonalen Terme in der Gewichtsmatrix zeigen an, dass jedes Neuron mit sich selbst mit einem positiven Gewicht von $1$ verbunden ist, was Selbstförderung bedeutet. Die Terme außerhalb der Diagonalen, \(-\epsilon\), sind negativ und stellen somit eine Hemmung dar.

In diesem anschaulichen Beispiel hat die Gewichtsmatrix die Form:

Eine gute Wahl von \(\epsilon\) wäre eine, die schnelle Konvergenz bietet.

Die Gleichungen, die den Wettbewerb beschreiben, sind:

wobei \(\textbf{a}^{2}(0)\), eine $S\times 1$-Spaltenvektormatrix, die Anfangsbedingung ist; die Ausgabe der rekurrenten Schicht (Schicht $2$) zum Zeitpunkt $t = 0$, die \(\text{a}^{1}\) der Ausgabe der Feedforward-Schicht (Schicht $1$) entspricht. Dann werden die zukünftigen Ausgaben des Netzes aus den vorherigen Ausgaben berechnet:

wobei \(\textbf{a}^{2}(t)\), $S\times 1$ Spaltenvektormatrix, die Ausgabe der rekurrenten Schicht zum Zeitpunkt (oder Iteration) $t = 1, 2, 3…$ ist.

Das bedeutet, dass bei jeder Iteration in der rekurrenten Schicht und für ein gegebenes Neuron $i = 1,…,S$ jedes Ausgabeelement \(a_{i}^{2}(t)\) um den gleichen Anteil des anderen Neurons $j$ reduziert wird; d.h. \(-\epsilon \ast a_{j}^{2}(t)\).

Im Allgemeinen ist die Nettoeingabe \(\text{n}_{i}^{2}(t)\), die das Neuron zum Zeitpunkt $t$ in seine Aktivierungsfunktion erhält:

und

Dabei wird davon ausgegangen, dass nur ein Neuron, nicht aber zwei oder mehr Neuronen, denselben maximalen Ausgabewert (d.h. seinen Aktivierungswert aufgrund der Aktivierungsfunktion) haben können. Da die Ausgänge (Aktivierungen) aufgrund der poslin-Aktivierungsfunktion alle nicht-negativ sind, ist es klar, dass für alle $i$: \(\text{n}_{i}^{2}(t)\le \text{a}_{i}^{2}(t-1)\), und so wie die rekurrente Schicht iteriert, nehmen die Aktivierungswerte aller Neuronen ab. Je kleiner jedoch ihre Aktivierungen sind, desto stärker nehmen sie ab. Bei der Iteration der rekurrenten Schicht werden die Neuronen mit den kleinsten Nettoeingaben \(\text{n}_{i}^{2}(t)\) zuerst ins Negative getrieben, d.h. das größere Element wird um weniger und das kleinere Element um mehr reduziert, so dass die Differenz zwischen groß und klein größer wird. Die Übertragungsfunktionen der Neuronen ergeben dann Nullwerte für ihre Aktivierungen. Sobald eine Aktivierung auf Null gesetzt wird, bleibt sie bei den folgenden Iterationen auf Null. Bis schließlich die Aktivierungen aller Neuronen bis auf eine, die des Gewinners, auf Null gesetzt werden. Die Aktivierung des Gewinners nimmt dann nicht mehr weiter ab. Die rekurrente Schicht bewirkt, dass alle Neuronenausgänge auf Null gesetzt werden, mit Ausnahme des Neurons mit dem größten Ausgabewert (der dem Prototypmuster entspricht, das der Eingabe in der Hamming-Distanz am nächsten ist).

Die Frage ist, wie groß der Wert für \(\epsilon\) sein kann, um eine schnelle Konvergenz zu erreichen.

• $\epsilon$ zu klein: braucht zu lange, um zu konvergieren (mehr Iterationen erforderlich)
• $\epsilon$ zu groß: kann das gesamte Netzwerk unterdrücken (es kann kein Gewinner gefunden werden, da alle Aktivierungen in einem einzigen Schritt auf Null gefahren werden)

Die schnellste Konvergenz kann erreicht werden, wenn ein $\epsilon$ so gewählt werden kann, dass die Aktivierungen aller Neuronen außer dem Gewinnerneuron in einer Iteration auf Null gefahren werden. Wenn bekannt ist, dass z.B. das Neuron $k$ den größten Endoutput \(a_{k}^{2}\) hat, dann wählt man $\epsilon$ etwas kleiner als \(\epsilon_{max}\):

dann wird in einer einzigen Iteration (zum Zeitpunkt $t$) die Nettoeingabe \(\text{n}_{k}^{2}(t)\) nur geringfügig größer als Null und daher wird ihre Aktivierung \(\text{a}_{k}^{2}(t)\) durch die Übertragungsfunktion poslin nur geringfügig größer als Null sein. Das bedeutet, dass alle anderen \(n_{i}^{2}(t)\) negativ werden und somit ihre Aktivierungswerte \(a_{i}^{2}(t)\) zu Null werden. Es ist jedoch nicht bekannt, welches der Neuronen die größte Aktivierung hat, und somit ist auch nicht bekannt, wie groß \(\epsilon_{max}\) ist. Deshalb wird \(\epsilon_{max}\) durch eine kleinere Zahl ersetzt und die rekurrente Schicht wird einige Male iteriert, bevor sie konvergiert. Diese kleinere Zahl ergibt sich aus der obigen Gleichung, indem der Nenner durch eine größere Zahl ersetzt wird.

Anhand praktischer Beispiele konnte festgestellt werden, dass:

mit \(j = 1,..,S \neq k\) und durch die Wahl des Falles \(\frac{a_{j}^{2}(0)}{a_{k}^{2}(0)}= 1\) wird der Nenner in der vorherigen Gleichung zu \(\sum_{j\neq k}^{S}\frac{a_{j}^{2}(0)}{a_{k}^{2}(0)} = S-1\). Damit ist \(\epsilon\) gewählt:

und dies führt zu einer etwas schnelleren Konvergenz, insbesondere wenn $S$ nicht zu groß ist.

Zur Veranschaulichung der Funktionsweise des Hamming-Netzes werden die beiden Prototyp-Muster betrachtet; Typ A, bei dem \(\textbf{p}_{\textbf{1}} = \left[\matrix{ 1\cr -1\cr 1} \right]\) und Typ B, bei dem \(\textbf{p}_{\textbf{2}} = \left[\matrix{ -1\cr -1\cr -1} \right]\), ein Eingabemuster \(\textbf{p} = \left[\matrix{ -1\cr 1\cr -1} \right]\) und unter Verwendung einer linearen Übertragungsfunktion wäre die Ausgabe der Feedforward-Schicht:

\(\text{a}^{1} = \left[ \left[\matrix{ 1 &-1& 1\cr -1 &-1 &-1} \right] \cdot \left[\matrix{-1 \cr 1 \cr -1}\right]+ \left[\matrix{ 3\cr 3} \right] \right]\) \(= \left[\matrix{ -3\cr 1}\right] +\left[\matrix{ 3\cr 3}\right] = \left[\matrix{ 0\cr 4} \right]\)

die dann zur Ausgabebedingung für die rekurrente Schicht wird.

Die Gewichtsmatrix für die rekurrente Schicht wird durch die folgende Gleichung gegeben:

wobei:

Jede Zahl für \(\epsilon\), die kleiner als $1$ ist, führt also zu einer schnelleren Konvergenz, zum Beispiel \(\epsilon = 0,5\).

Die erste Iteration $(t=1)$ der rekurrenten Schicht ergibt:

Die zweite Iteration $(t=2)$ ergibt:

Da die Ausgänge der aufeinanderfolgenden Iterationen das gleiche Ergebnis liefern, ist das Netz konvergiert. Prototyp Nummer zwei, das Typ B-Paket, wird als die korrekte Übereinstimmung ausgewählt, da Neuron Nummer zwei die einzige Ausgabe ungleich Null hat. Dies ist die richtige Wahl, da die Hamming-Distanz zwischen dem Prototyp vom Typ A und dem Eingabemuster $3$ und die Hamming-Distanz zwischen dem Prototyp vom Typ B und dem Eingabemuster $1$ beträgt.

Dieser Entwurf eines Hamming-Netzwerks kann in MATLAB wie folgt kodiert werden:

was zu der folgenden Ausgabe führt:

5. Hopfield Netzwerk

Das Hopfield-Netz ist ein rekurrentes Netz, das in mancher Hinsicht der rekurrenten Schicht des Hamming-Netzes ähnelt, aber effektiv die Operationen beider Schichten des Hamming-Netzes ausführen kann.

Es besteht aus $S$ Neuronen, was der Anzahl der Elemente im Eingabevektor entspricht. Die Neuronen werden mit dem Eingabevektor $p$ initialisiert, der eine $Sx1$-Spaltenvektormatrix ist:

dann iteriert das Netzwerk so lange, bis die Ausgabe $\textbf{a}(t)$, ebenfalls eine $Sx1$-Spaltenvektormatrix, konvergiert, was zu einer Ausgabe führt, die einer der Prototyp-Vektoren sein sollte.

wobei satlins die Übertragungsfunktion ist. Es handelt sich um eine sättigende lineare Übertragungsfunktion; sie ist im Bereich $[-1, 1]$ linear und sättigt bei $1$ für Eingaben größer als $1$ und bei $-1$ für Eingaben kleiner als $-1$.

Im Gegensatz zum Hamming-Netz, bei dem das Neuron ungleich Null anzeigt, welches Prototyp-Muster ausgewählt wird, produziert das Hopfield-Netz an seinem Ausgang tatsächlich das ausgewählte Prototyp-Muster.

Das Verfahren zur Berechnung der Gewichtsmatrix und des Bias-Vektors für das Hopfield-Netz ist komplexer als für das Hamming-Netz, bei dem die Gewichte in der Feedforward-Schicht die Prototypmuster sind.

Für dieses anschauliche Beispiel werden die Gewichtsmatrix und der Bias-Vektor so bestimmt, dass dieses spezielle Mustererkennungsproblem gelöst werden kann. Zum Beispiel könnten die folgenden Gewichte und Bias verwendet werden:

Die Netzwerkausgabe muss entweder gegen das Muster Typ A, \(\textbf{p}_{\textbf{1}} = \left[\matrix{ 1\cr -1\cr 1} \right]\), oder gegen das Muster Typ B, \(\textbf{p}_{\textbf{2}} = \left[\matrix{ -1\cr -1\cr -1} \right]\), konvergieren. In beiden Mustern ist das zweite Element $-1$. Der Unterschied zwischen den Mustern besteht im ersten und dritten Element. Unabhängig davon, welches Muster in das Netz eingegeben wird, muss daher das zweite Element des Ausgabemusters gegen $-1$ konvergieren, während das erste und das dritte Element entweder gegen $1$ oder $-1$ konvergieren, je nachdem, was näher am ersten bzw. dritten Element des Eingangsvektors liegt.

Die Funktionsgleichungen des Hopfield-Netzes lauten unter Verwendung der oben genannten Parameter wie folgt:

Das bedeutet, dass unabhängig von den Anfangswerten, $\text{a}_{i}(0)$, das erste und das dritte Element mit einer Zahl größer als $1$ multipliziert werden. Wenn also der Anfangswert dieses Elements negativ ist, wird es schließlich bei $-1$ in Sättigung gehen; andernfalls wird es bei $1$ in Sättigung gehen. Das zweite Element wird verringert, bis es bei $-1$ in Sättigung geht.

Betrachtet man wie zuvor das Eingabemuster des nicht ganz perfekten Pakets vom Typ B, $\textbf{p} = \left[\matrix{ -1\cr 1\cr -1} \right]$, um das Hopfield-Netz zu testen, so würden die Ausgaben für die ersten drei Iterationen lauten:

\(\textbf{a}(0) = \left[\matrix{ -1\cr 1\cr -1} \right], \ \textbf{a}(1) = \left[\matrix{ -1\cr -0.7\cr -1} \right],\) \(\textbf{a}(2) = \left[\matrix{ -1\cr -1\cr -1} \right], \ \textbf{a}(3) = \left[\matrix{ -1\cr -1\cr -1} \right]\)

Das Netz konvergierte zum Parzellenmuster des Typs B, ebenso wie das Hamming-Netz und das Perzeptron, obwohl jedes Netz auf unterschiedliche Weise arbeitete. Das Perzeptron hatte einen einzigen Ausgang, der die Werte $-1$ (Typ B-Parzelle) oder $1$ (Typ A-Parzelle) annehmen konnte. Im Hamming-Netz zeigte das einzelne Neuron ungleich Null an, welches Prototyp-Muster die ähnlichste Übereinstimmung aufwies. Wenn das erste Neuron ungleich Null war, bedeutete dies eine Parzelle vom Typ A, und wenn das zweite Neuron ungleich Null war, bedeutete dies ein Muster vom Typ B. Im Hopfield-Netz erscheint das Prototyp-Muster selbst am Ausgang des Netzes.

Dieses Hopfield-Netzwerk kann in MATLAB wie folgt kodiert werden:

was zu der folgenden Ausgabe führt:

Klassifizierung von linear trennbaren Daten mit einem Perzeptron

Problembeschreibung

In diesem Beispiel gibt es zwei Datencluster mit jeweils $20$ Stichproben, die zu zwei Klassen gehören. Diese Cluster sind in einem zweidimensionalen Eingaberaum definiert. Die Klassen sind linear trennbar.

Ziel

Konstruktion eines Perzeptrons für die Klassifizierung von zwei zufällig definierten Datenclustern.

Schritte

1. Definition von Eingabe- und Ausgabedaten
2. Erstellung und Training des Perzeptrons
3. Einzeichnen der Entscheidungsgrenze

1. Definition von Eingabe- und Ausgabedaten

Zunächst werden mit der MATLAB-Funktion randn, welche normalverteilte Zufallszahlen erzeugt, $20$ Stichprobenvektoren zweier verschiedener Klassen zufällig definiert. Den Stichproben der zweiten Klasse wird ein Offset von $5$ hinzugefügt, damit sie einen unterscheidbaren Abstand zu den Stichproben der ersten Klasse haben. Jede Klasse wird als $2$-mal-$20$-Matrix festgelegt und zu einer $2$-mal-$40$-Matrix $p$ zusammengefasst. Die Matrix $p$ stellt also die Eingaben für das Perzeptron dar: normalverteilte Zufallszahlen, eine $2$-mal-$40$ ($R$-mal-$Q$)-Matrix von $40$ Eingabevektoren mit jeweils zwei Elementen.

Um die Vektoren in der Matrix $p$ einer der beiden Klassen zuzuordnen, wird eine zweite Matrix, $t$, als $1$-mal-$40$ ($S$-mal-$Q$) Ausgabematrix definiert. Die ersten $20$-Elemente der $t$-Matrix werden mit dem Wert Null und die anderen $20$-Elemente mit dem Wert Eins belegt. Die Ausgabematrix $t$ besteht also aus $40$ Zielvektoren, die jeweils aus einem einzigen Element (entweder Null oder Eins) bestehen.

Um die Eingabe- und Zielvektoren des Perzeptrons darzustellen, wird die Funktion plotpv verwendet, die zwei Argumente benötigt: das erste ist die Eingabematrix und das zweite die Zielmatrix. Damit werden Spaltenvektoren in der Eingabematrix mit Markierungen auf der Grundlage der Ausgabematrix gezeichnet.

Der obige Code stellt die Stichproben dar:

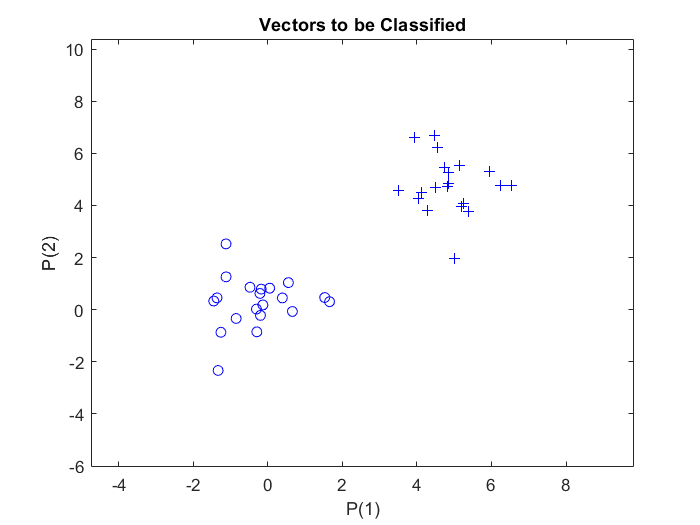
2. Erstellung und Training des Perzeptrons

In MATLAB wird ein Einschicht-Perzeptron mit dem Befehl: net = perceptron; erstellt.

Das Perzeptron verwendet standardmäßig eine Hard-Limit-Übertragungsfunktion, hardlim.

Die Trainingsfunktion für Perzeptron ist standardmäßig auf trainc eingestellt, was ein zyklisches Gewichts-/Bias-Training ist, und wird durch train aufgerufen. trainc trainiert ein Netzwerk mit Gewichts- und Bias-Lernregeln mit inkrementellen Updates nach jeder Präsentation einer Eingabe. Die Eingaben werden in zyklischer Reihenfolge präsentiert. Das Training stoppt, wenn eine dieser Bedingungen erfüllt ist:

• Die maximale Anzahl von Epochen (Wiederholungen) ist erreicht.
• Die Leistung wird auf das Ziel minimiert.
• Die maximale Zeitspanne wird überschritten.

Zur Messung der Netzleistung wird standardmäßig die Funktion des mittleren absoluten Fehlers, mae, verwendet. Der Fehler wird durch Subtraktion des Ausgangs vom Ziel berechnet. Dann wird der mittlere absolute Fehler berechnet. Das Ziel ist die Minimierung der Leistung, d.h. des Fehlers.

Als Ergebnis des obigen Codes wird die Trainingsaufzeichnung mit den Trainings- und Leistungsfunktionen und -parametern sowie dem Wert der besten Leistung (dem erreichten Mindestfehler) angezeigt.

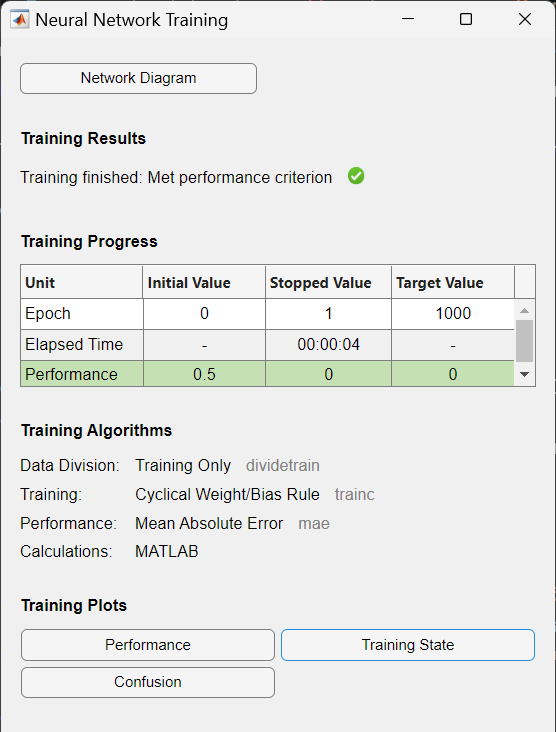
view(net) öffnet ein Fenster, das das neuronale Netz (angegeben durch net) als grafisches Diagramm darstellt. Die Zahlen zeigen an, dass die Eingabevektoren zwei Elemente enthalten, das Netz aus einer Schicht mit einem einzigen Neuron besteht und eine Hard-Limit-Übertragungsfunktion verwendet, und die Ausgabe ein Einzelelementvektor ist.

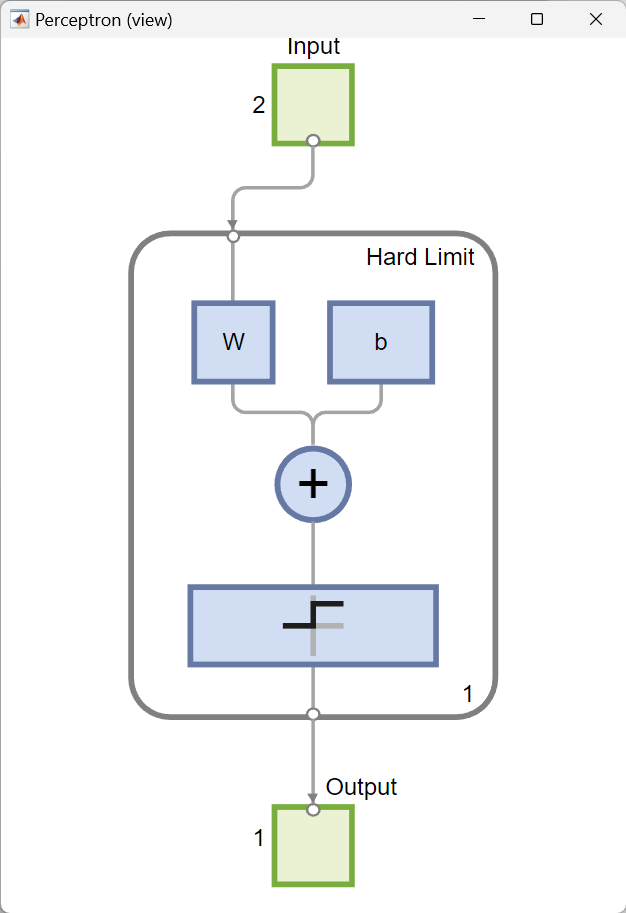
3. Einzeichnen der Entscheidungsgrenze

Nachdem das Netz trainiert wurde, wird im nächsten Schritt die Klassifizierungslinie auf dem zuvor gezeichneten Perzeptron-Vektorplot dargestellt. Dies geschieht mit der Funktion plotpc, die zwei Argumente als Eingabe benötigt:

• Die erste ist die $S$-mal-$R$-Gewichtsmatrix, net.iw{1,1}, die die endgültige Gewichtsmatrix nach dem Training ist. \(\left\{ 1,1 \right\}\) bezeichnet die Gewichte für die Verbindung vom ersten Eingang zur ersten Schicht,
• und das zweite Argument ist der $S$-mal-$1$ Bias-Vektor, net.b{1}, der der endgültige Bias-Vektor nach dem Training für die erste Schicht ist.

Dabei ist $S$ die Anzahl der Neuronen in der Schicht und $R$ die Anzahl der Elemente im Eingabevektor.

Schließlich wird die lineare Entscheidungsgrenze eingezeichnet, die die Datenpunkte, die zu den beiden Klassen gehören, voneinander trennt:

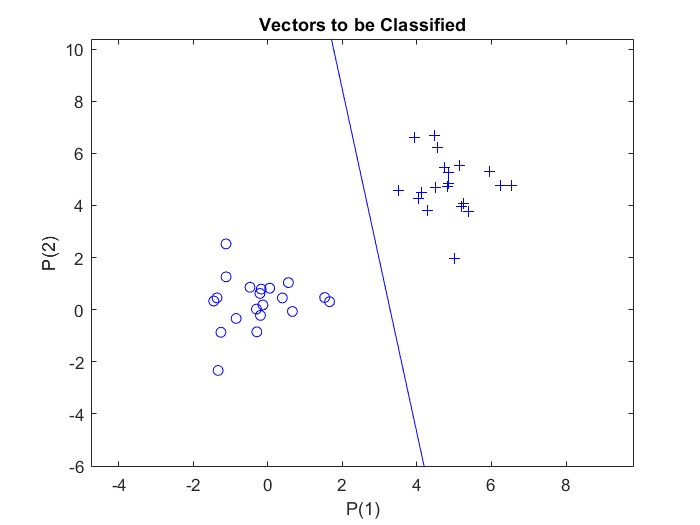
Benutzerdefinierte neuronale Netze

Problembeschreibung und Ziel

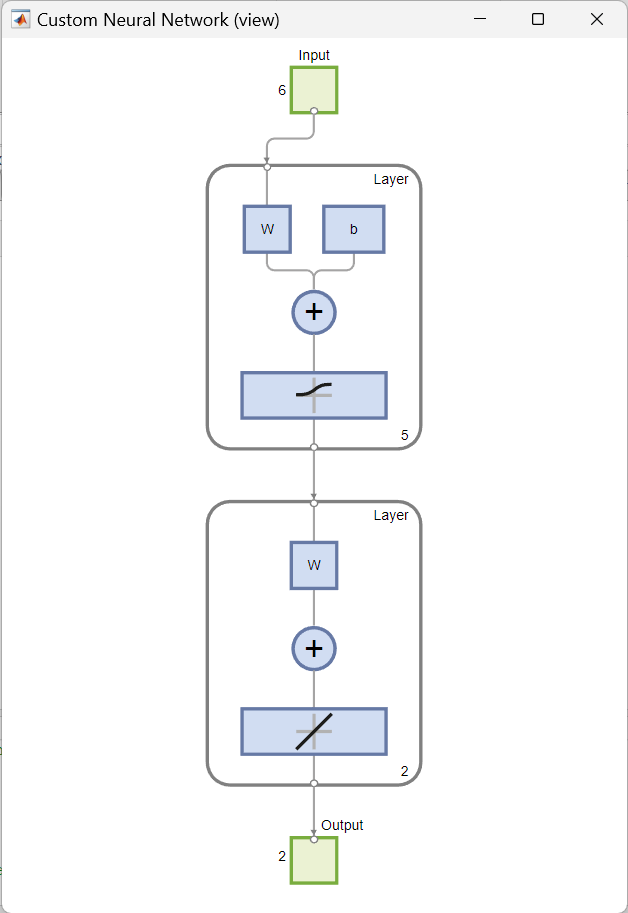
Dieses Beispiel zeigt, wie ein benutzerdefiniertes, untiefes neuronales Netz in MATLAB mit Hilfe der Netzwerkfunktion erstellt und angezeigt wird. Das zu erstellende Netz ist ein Feedforward-Netz, das aus zwei Schichten besteht. Es hat einen einzelnen Eingabevektor mit sechs Elementen und einen Ausgabevektor (“Zielausgabe”) mit zwei Elementen. Nur die erste Schicht hat einen Bias. Ein Eingabegewicht verbindet die erste Schicht mit der Eingabe. Ein Schichtgewicht verbindet sich von der ersten Schicht aus mit der zweiten Schicht. Die zweite Schicht ist der Ausgang des Netzes.

Schritte

1. Definition der Eingaben und Ausgaben
2. Definition und Anpassung des Netzes (Anzahl der Teilobjekte des Netzes)
3. Festlegung der Topologie (Eigenschaften der Teilobjekte des Netzes) und der Übertragungsfunktion
4. Konfigurieren des Netzwerks mit configure
5. Training des Netzes und Berechnung der Neuronenausgabe

1. Definition der Eingaben und Ausgaben

Der obige Code erstellt die Eingabe- und Ausgabe- (Ziel-) Vektoren.

2. Definition und Anpassung des Netzes (Anzahl der Teilobjekte des Netzes)

Um ein benutzerdefiniertes untiefes neuronales Netz mit einer Eingabe und zwei Schichten zu erstellen, wird der folgende Codeausschnitt verwendet. Die Anzahl der Eingaben bestimmt, wie viele Sätze von Vektoren das Netz als Eingabe erhält. Die Größe der einzelnen Eingaben (d. h. die Anzahl der Elemente in jedem Eingabevektor) wird durch die Eingabegröße bestimmt (in diesem Beispiel gibt es einen Eingabevektor, also net.numInputs = 1 und die Eingabegröße ist net.inputs{1}.size = 6).

Syntax:

net = network(numInputs,numLayers,biasConnect,inputConnect,layerConnect,outputConnect)

• numInputs: Anzahl der Eingaben, die das Netz erhält (wie viele Sätze von Vektoren das Netz als Eingabe erhält)
• numLayers: Anzahl der Schichten, die das Netz hat (hier: zwei Schichten)
• biasConnect: numLayers-mal-$1$ Boolescher Vektor; diese Eigenschaft legt fest, welche Schichten Bias haben ($1$ bedeutet Vorhandensein und $0$ bedeutet Abwesenheit) (hier: die erste Schicht hat einen)
• inputConnect: numLayers-mal-numInputs Boolesche Matrize; diese Eigenschaft definiert, welche Schichten Gewichte haben, die von Eingaben stammen (hier: die erste Schicht hat eines)
• layerConnect: numLayers-mal-numLayers Boolesche Matrize; diese Eigenschaft definiert, welche Schichten Gewichte von anderen Schichten haben (hier: zweite Schicht hat ein Gewicht, das von der ersten Schicht zur zweiten Schicht kommt)
• outputConnect: $1$-mal-numLayers Boolescher Vektor; diese Eigenschaft legt fest, welche Schichten Netzausgaben erzeugen (hier: die zweite Schicht)

Das Ergebnis ist eine grafische Darstellung der Struktur des festgelegten benutzerdefinierten neuronalen Netzes:

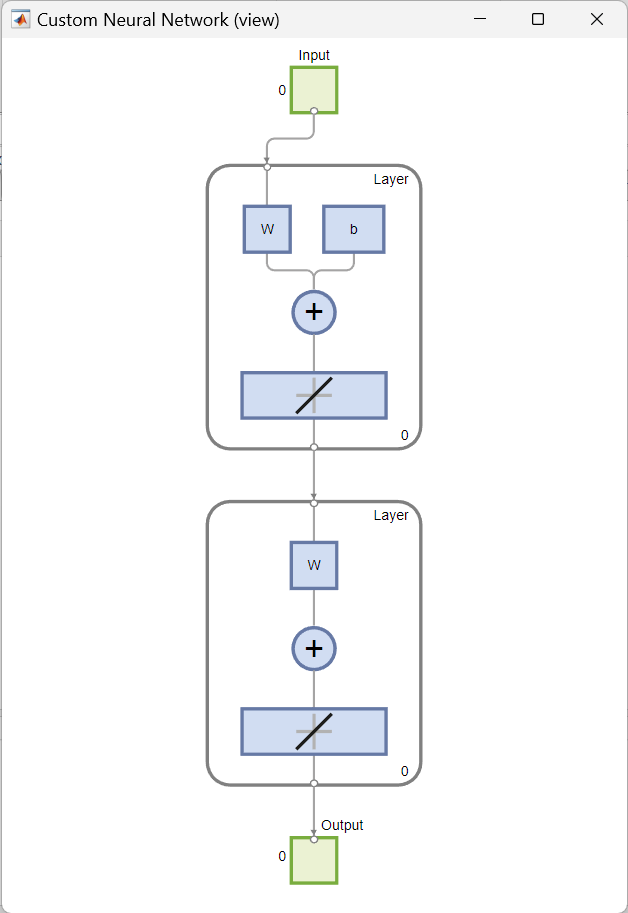
3. Festlegung der Topologie (Eigenschaften der Teilobjekte des Netzes) und der Übertragungsfunktion

Der nächste Schritt besteht darin, die Anzahl der Neuronen in jeder Schicht festzulegen. In diesem Fall werden der ersten Schicht $5$ Neuronen zugewiesen und der zweiten Schicht keine. Dann wird der ersten Schicht die logistische Sigmoid-Übertragungsfunktion, logsig, zugewiesen. Der zweiten Schicht wird standardmäßig eine lineare Übertragungsfunktion, purelin, zugewiesen.

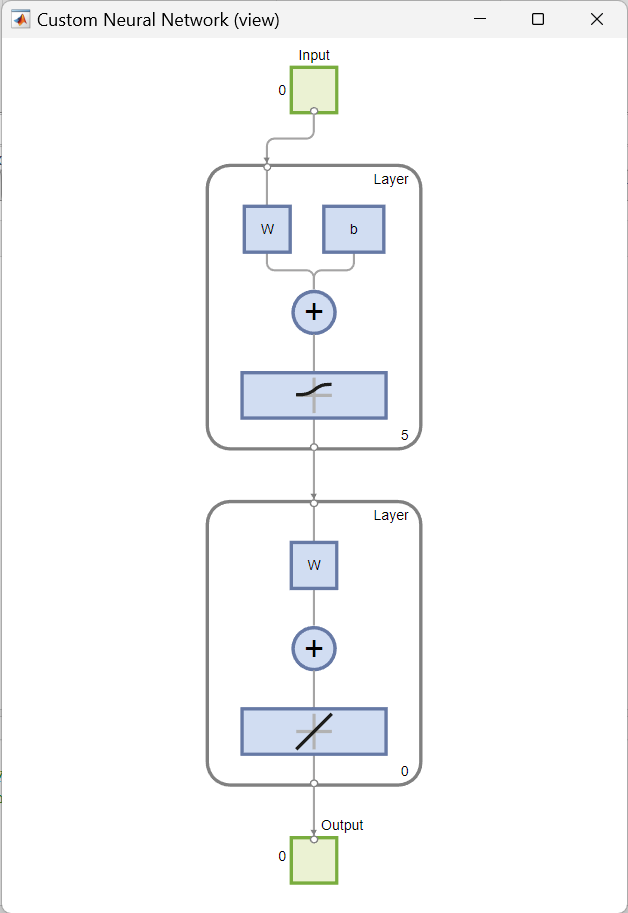
4. Konfigurieren des Netzwerks mit configure

Bei der Konfiguration werden die Eingabe- und Ausgabegröße und -bereiche des Netzes, die Einstellungen für die Vorverarbeitung der Eingaben und die Nachverarbeitung der Ausgaben sowie die Einstellungen für die Initialisierung der Gewichte so festgelegt, dass sie den Eingabe- und Zieldaten entsprechen.

Die Funktion configure konfiguriert die Eingaben und Ausgaben des Netzes so, dass sie den Eingabe- und Zieldaten am besten entsprechen. Sie nimmt Eingabedaten (hier: inputs) und Zieldaten (hier: outputs) und konfiguriert die Eingänge und Ausgänge des Netzes so, dass sie übereinstimmen. In diesem Beispiel ist das Netz so konfiguriert, dass die Ausgaben der zweiten Schicht lernen, mit den zugehörigen Zielvektoren übereinzustimmen.

Die Konfiguration muss erfolgen, bevor die Gewichte und Biases eines Netzes initialisiert werden können. Unkonfigurierte Netze werden automatisch konfiguriert und initialisiert, wenn train zum ersten Mal aufgerufen wird.

5. Training des Netzes und Berechnung der Neuronenausgabe

Nach der Konfiguration und vor dem Training werden die Gewichte und Biases des Netzes initialisiert, indem die Ausgabe des Netzes für den gegebenen Eingabevektor berechnet wird.

Dies ist die Ausgabe des Netzwerks vor dem Training:

Auf die Initialisierung folgt das Training des Netzes mit einer geeigneten Trainingsfunktion. In diesem Fall wird die Levenberg-Marquardt-Backpropagation (trainlm) als Trainingsfunktion verwendet, so dass bei einem beispielhaften Eingabevektor die Ausgaben der zweiten Schicht lernen, dem zugehörigen Zielvektor mit minimalem mittleren quadratischen Fehler (mse) zu entsprechen.

Die Trainingsaufzeichnung wird angezeigt:

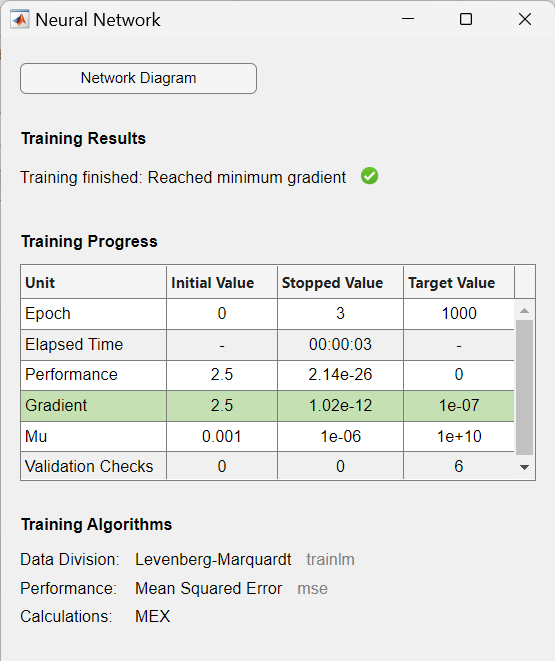
und die Ausgabe des trainierten Netzes ist der gewünschte (Ziel-)Vektor:

Industrielle Fehlerdiagnose von Pleuelstangen in Kompressoren

Problembeschreibung

Die Pleuelstange in einem Kompressor ist ein wichtiger Faktor, um die Zuverlässigkeit eines Kompressors zu gewährleisten. Sie verbindet die Kurbelwelle mit dem Kolben und bewegt sich in einer linearen Hin- und Herbewegung entlang der Mitte des Kolbens im Inneren des Zylinders. Sie ist während des Betriebs des Kompressors einer periodisch wechselnden Belastung ausgesetzt.

In diesem Beispiel werden gegossene Pleuelstangen betrachtet. Eine häufige Ursache für das Versagen dieser Stangen ist die strukturelle Überlastung aufgrund enormer Zugbelastungen durch größere Trägheitskräfte, die auf die Stangen ausgeübt werden. Eine weitere Ursache für das Versagen von Pleuelstangen ist die Entstehung von Mikrorissen im Metall durch konzentrierte Spannungen aufgrund von Unvollkommenheiten an der Stange, die schließlich zu einem Bruch führen, der die Stange zum Brechen bringt.

Es wird ein Datensatz aus $2000$ Stichproben von Pleuelstangen erstellt, der die aufgezeichneten periodischen Werte in $100$ Intervallen der sich ändernden Belastung auf jede Pleuelstange und den jeweiligen Qualitätszustand der Stange enthält, der wiederum in drei Klassen unterteilt wird: Die erste Klasse umfasst die unbeschädigt gebliebenen Pleuelstangen (“OK”-Fälle), die zweite Klasse umfasst Pleuelstangenversagen aufgrund von “Überlast” (“overload”) und die dritte Klasse umfasst Pleuelstangenversagen aufgrund von “Riss” (“crack”).

Ziel

Die Aufgabe besteht darin, für jedes geprüfte Pleuel zu erkennen, ob es sich um ein defektes Pleuel (aufgrund eines Risses oder einer Überlastung) handelt oder nicht, und zwar anhand der gesammelten Daten der gemessenen periodischen Belastungswerte, denen das geprüfte Pleuel ausgesetzt war.

Schritte

Zur Erfüllung dieser Aufgabe wird ein mehrschichtiges Perzeptron verwendet, und die folgenden Schritte werden zur Vor- und Nachbearbeitung der Daten sowie zur Erstellung und Konfiguration des Netzes durchgeführt:

1. Laden und Darstellen der Daten
2. Vorbereiten der Eingaben: Konvertierung der Datenabtastrate
3. Festlegung der binären Ausgabekodierung: 0=OK, 1=Error
4. Erstellung und Training eines mehrschichtigen Perzeptrons
5. Post-Training-Analyse und Bewertung der Netzwerkleistung
6. Anwendung

1. Laden und Darstellen der Daten

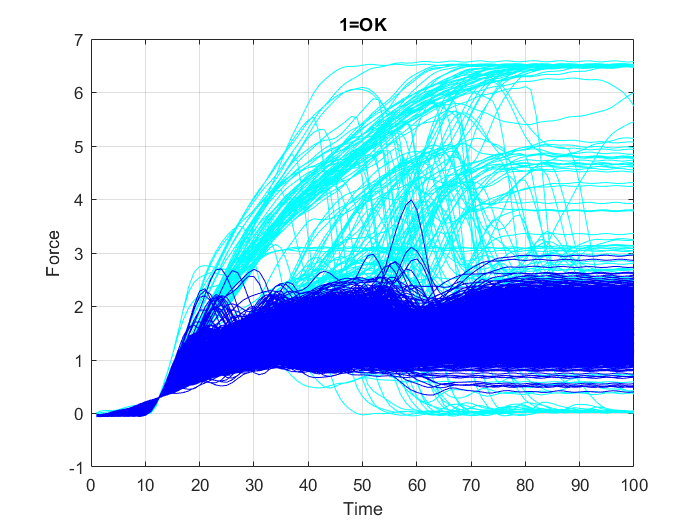
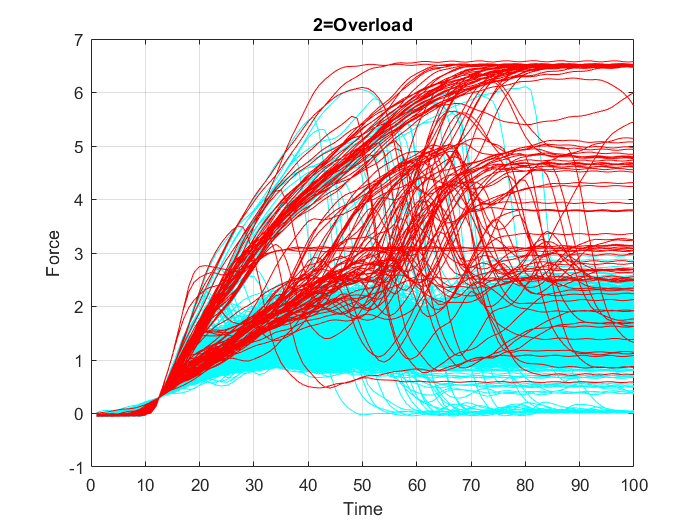
Zunächst werden alle Variablen aus dem Datensatz “data.mat” in den MATLAB-Arbeitsbereich geladen. Zur Überprüfung des Inhalts des Arbeitsbereichs, d. h. der Namen, Größen und Typen aller Variablen im Datensatz, wird die Funktion whos verwendet. Anschließend werden die Daten in drei separaten Diagrammen (Abbildung 18, Abbildung 19 und Abbildung 20) dargestellt. In jedem dieser Diagramme sind die Datenpunkte, die nur zu einer der drei Klassen (“OK”, “Überlast” (“Overload”) oder “Riss” (“Crack”)) gehören, in einer bestimmten Farbe hervorgehoben, während die anderen Punkte in Cyan dargestellt werden.

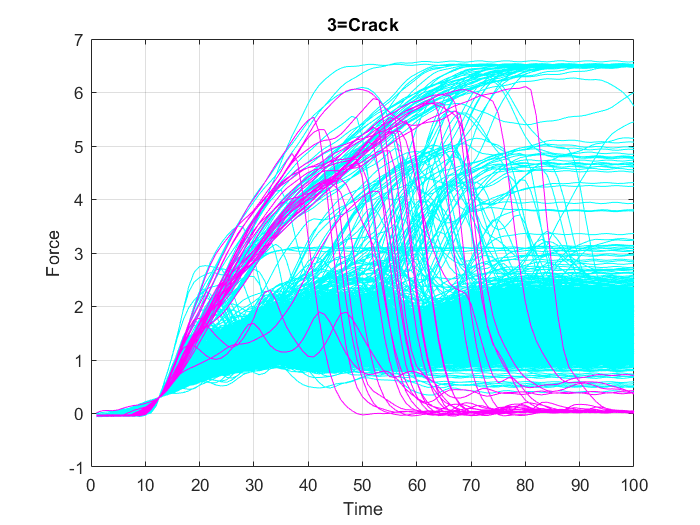
2. Vorbereiten der Eingaben: Konvertierung der Datenabtastrate

In diesem Fall ist es nicht notwendig, die volle Auflösung der Zeitreihendaten zu verwenden. Um die für das Modelltraining erforderlichen Rechenressourcen zu reduzieren, wird daher ein Downsampling der Eingabedaten durchgeführt, das das Training auf einer unverhältnismäßig kleinen Teilmenge der Beispiele der Mehrheitsklasse ermöglicht. Zu diesem Zweck werden die Eingabedaten dezimiert, d. h. die Stichprobenhäufigkeit wird um den Faktor $10$ reduziert, so dass nur jede zehnte Stichprobe erhalten bleibt. Abbildung 21, Abbildung 22 und Abbildung 23 zeigen die Graphen der neu abgetasteten Datenpunkte.

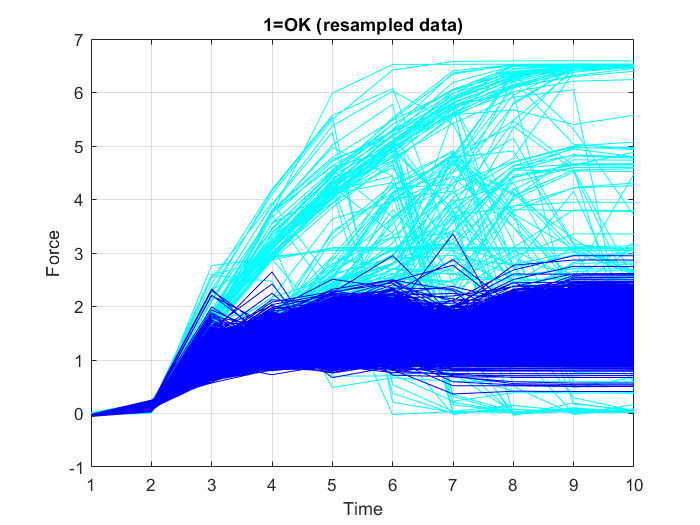
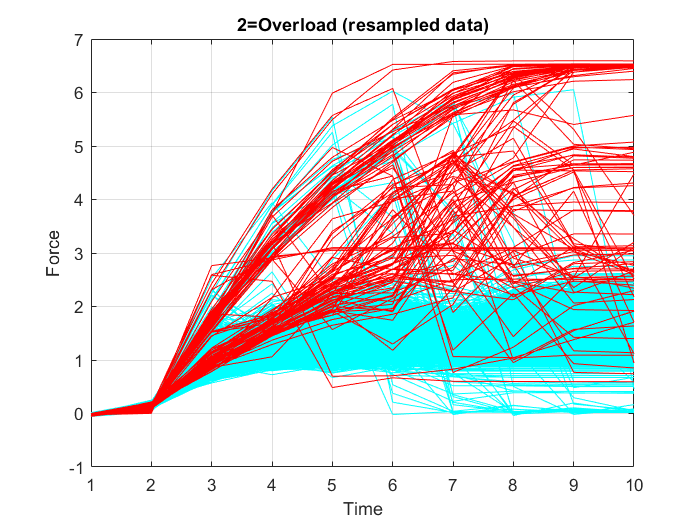
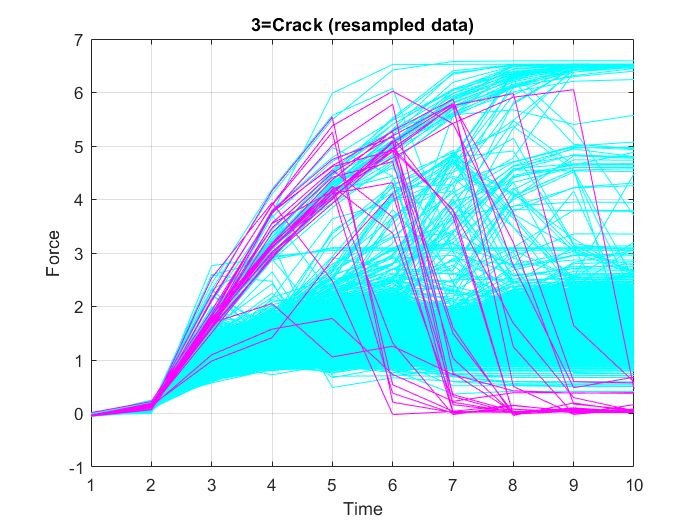
3. Festlegung der binären Ausgabekodierung: 0=OK, 1=Error

Nach der Abtastratenkonvertierung der Eingabedaten werden die Zieldaten mit Hilfe einer bedingten Anweisung in die beiden Klassen “OK” und “Error” umgewandelt. Diese Anweisung durchläuft alle Werte der Zellen innerhalb des Zieldatenblatts nacheinander und gibt einen wahren oder falschen Zustand zurück, der durch die Zahlen $1$ bzw. $0$ repräsentiert wird, wenn der Wert der geprüften Zelle größer als eins ist (Klasse “Error”) bzw. nicht (Klasse “OK”).

4. Erstellung und Training eines mehrschichtigen Perzeptrons

Mit der MATLAB-Funktion feedforwardnet wird ein Feedforward-Netz erstellt, um die Eingabe- und Ausgabedaten abzubilden. Sie erzeugt ein Feedforward-Netz, das aus einer Reihe von Schichten besteht. Die erste Schicht ist mit der Eingabe des Netzes verbunden. Jede nachfolgende Schicht hat eine Verbindung von der vorherigen Schicht. Die letzte Schicht erzeugt die Ausgabe des Netzes. Die Größe (Anzahl der Neuronen) der versteckten Schichten des Netzes wird als Zeilenvektor angegeben. Die Länge des Vektors bestimmt die Anzahl der versteckten Schichten im Netz. Die Eingabe- und Ausgabegrößen werden auf Null gesetzt. Die Software passt die Größen dieser Schichten während des Trainings entsprechend den Trainingsdaten an.

In diesem Fall besteht das erstellte Feedforward-Netzwerk aus einer einzigen versteckten Schicht der Größe $4$ (vier Neuronen in der Schicht).

Anschließend wird der gesamte Datensatz in drei Teile aufgeteilt: Training, Validierung und Test.

1. Die Trainingsmenge wird zur Berechnung von Gradienten und zur Bestimmung von Gewichtsaktualisierungen verwendet.
2. Der Validierungssatz wird verwendet, um das Training zu beenden, bevor es zu einer Überanpassung kommt. Der Fehler in der Validierungsmenge wird während des Trainings überwacht. Der Validierungsfehler nimmt normalerweise in der Anfangsphase des Trainings ab, ebenso wie der Fehler des Trainingssets. Wenn das Netz jedoch beginnt, die Daten zu überanpassen, steigt der Fehler in der Validierungsmenge normalerweise an. Die Netzgewichte und Biases werden auf dem Minimum des Validierungssatzfehlers gespeichert.
3. Der Testsatz wird verwendet, um die zukünftige Leistung des Netzes vorherzusagen. Die Leistung des Testsatzes ist das Maß für die Qualität des Netzes. Wenn nach dem Training eines Netzes die Leistung des Testsatzes nicht ausreichend ist, gibt es in der Regel vier mögliche Ursachen:
   • Das Netz hat ein lokales Minimum erreicht,
   • das Netz hat nicht genügend Neuronen, um die Daten zu erfassen,
   • das Netz passt sich zu stark an, oder
   • das Netz extrapoliert.

Der Testsatzfehler wird nicht während des Trainings verwendet, sondern dient zum Vergleich verschiedener Modelle. Es ist auch nützlich, den Fehler des Testsatzes während des Trainingsprozesses aufzuzeichnen. Erreicht der Fehler im Testsatz ein Minimum bei einer deutlich anderen Iterationszahl als der Fehler im Validierungssatz, könnte dies auf eine schlechte Aufteilung des Datensatzes hinweisen.

In der Regel werden bei der Aufteilung der Daten etwa $70\%$ für das Training, $15\%$ für die Validierung und $15\%$ für die Tests verwendet.

Wenn die Netzgewichte und Biases initialisiert sind, ist das Netz bereit für das Training. Zum Trainieren des Netzes wird die MATLAB-Funktion train verwendet. Diese Funktion verwendet das Batch-Training (Aktualisierung der Gewichte nach der Präsentation des gesamten Datensatzes), um es vom inkrementellen Training (Aktualisierung der Gewichte nach der Präsentation jeder einzelnen Stichprobe) zu unterscheiden, das mit der MATLAB-Funktion adapt durchgeführt werden kann. Der Standard-Trainingsalgorithmus, der von train aufgerufen wird, ist Levenberg-Marquardt trainlm. Der Trainingsprozess erfordert eine Reihe von Beispielen für das richtige Verhalten des Netzes, d.h. die Netzeingänge force und die Zielausgänge target. Der Trainingsprozess beinhaltet die Abstimmung der Werte der Gewichte und Verzerrungen des Netzes, um die Leistung des Netzes zu optimieren, wie durch die Netzleistungsfunktion definiert. In der Regel wird eine Trainingsepoche als eine einzige Präsentation aller Eingabevektoren für das Netz definiert. Das Netz wird dann entsprechend den Ergebnissen all dieser Präsentationen aktualisiert. Die Standard-Leistungsfunktion für Feedforward-Netze ist der mittlere quadratische Fehler mse, d. h. der durchschnittliche quadratische Fehler zwischen den Netzausgaben $Y$ und den Zielausgaben target.

Während des Trainings wird der Fortschritt ständig im Trainingsfenster aktualisiert. Von größtem Interesse sind die Leistung, die Größe des Gradienten der Leistung und die Anzahl der Validierungsprüfungen. Die Größe des Gradienten und die Anzahl der Validierungsprüfungen werden verwendet, um das Training zu beenden. Der Gradient wird sehr klein, wenn das Training ein Minimum der Leistung erreicht. Wenn die Größe des Gradienten kleiner als $1e-5$ ist, wird das Training abgebrochen. Die Anzahl der Validierungsprüfungen gibt die Anzahl der aufeinanderfolgenden Iterationen an, bei denen die Validierungsleistung nicht abnimmt. Wenn diese Zahl $6$ (der Standardwert) erreicht, wird das Training abgebrochen.

Als Ergebnis wird die Trainingsaufzeichnung mit den Trainings- und Leistungsfunktionen und -parametern sowie dem Wert der besten Leistung (dem erreichten Mindestfehler) angezeigt. In diesem Fall hat die Anzahl der Validierungsprüfungen $6$ erreicht (der Standardwert), und das Training wurde daraufhin abgebrochen.

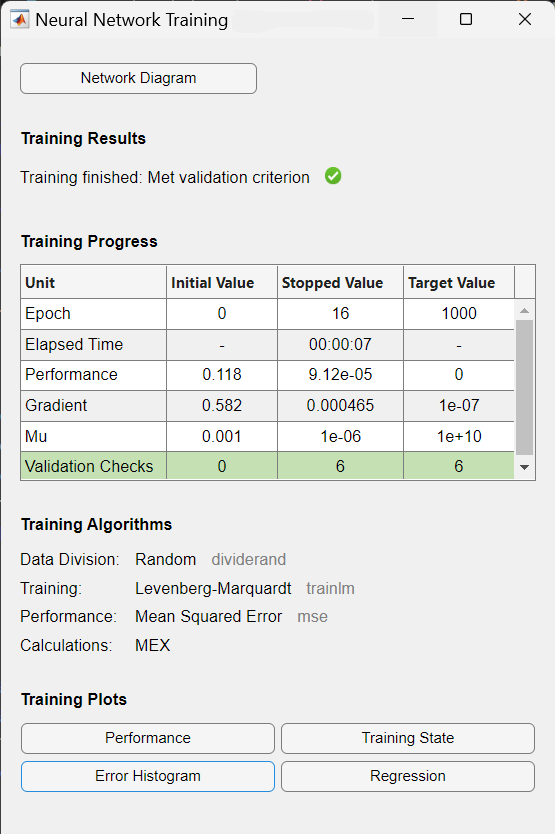
5. Post-Training-Analyse und Bewertung der Netzwerkleistung

Bevor ein trainiertes neuronales Netz verwendet wird, sollte es analysiert werden, um festzustellen, ob das Training erfolgreich war. Es gibt viele Techniken für die Analyse nach dem Training. Die gebräuchlichsten sind im Trainingsfenster zu finden, wo vier Diagramme verfügbar sind: Leistung, Trainingszustand, Fehlerhistogramm und Regression. Das Leistungsdiagramm zeigt den Wert der Leistungsfunktion in Abhängigkeit von der Iterationszahl. Sie stellt die Trainings-, Validierungs- und Testleistung dar. Wenn es keine größeren Probleme mit dem Training gibt, dann sind die Fehlerprofile für Validierung und Test sehr ähnlich. Wenn die Validierungskurve deutlich ansteigt, ist es möglich, dass eine Überanpassung stattgefunden hat. Die Darstellung des Trainingszustands zeigt den Fortschritt anderer Trainingsvariablen, wie die Größe des Gradienten, die Anzahl der Validierungsprüfungen usw. Die Darstellung des Fehlerhistogramms zeigt die Verteilung der Netzwerkfehler. Das Regressionsdiagramm zeigt eine Regression zwischen den Netzausgaben und den Netzzielen. In einem perfekten Trainingsfall wären die Netzausgaben und die Ziele genau gleich, aber das ist in der Praxis selten der Fall.

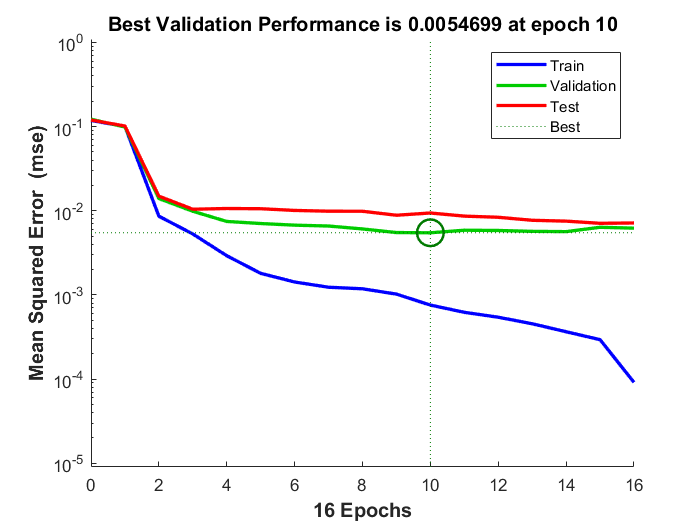
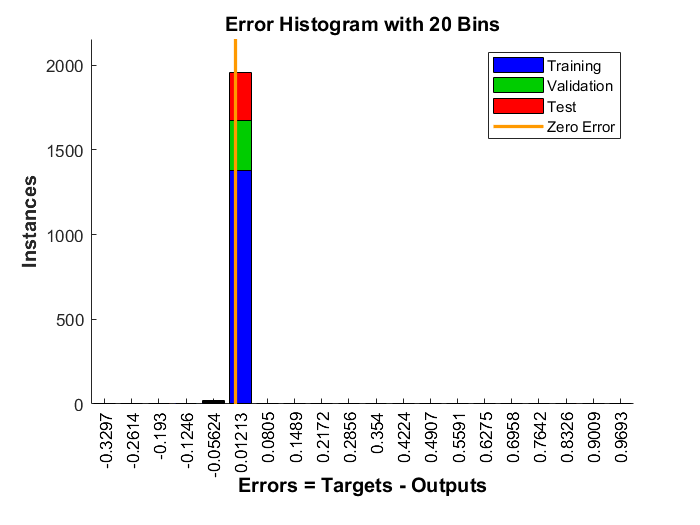
Aus der Trainingsaufzeichnung konnten das Leistungsdiagramm, Abbildung 25, und das Fehlerhistogramm, Abbildung 26, angezeigt werden. Das Leistungsdiagramm zeigt, dass bei Epoche $10$ die beste Leistung für den Validierungsdatensatz erreicht wurde und das Training gestoppt wurde, als die Anzahl der Validierungsprüfungen, bei denen die Validierungsleistung nicht abnimmt, $6$ erreichte, und weil die Fortsetzung des Trainings über diesen Punkt hinaus zu einer Überanpassung führt. Der Leistungswert für den Validierungsdatensatz ist der Durchschnitt der Fehlerquadrate, und der Fehler ist die Differenz zwischen der Ausgabe des Netzes (der beobachteten Ausgabe) und der Zielausgabe (der vorhergesagten Ausgabe). Ein kleinerer Fehler bedeutet, dass die Ausgaben sehr nahe an den Zielwerten liegen. Das Fehlerhistogramm zeigt die Fehler zwischen den Zielwerten und den Ausgabewerten nach dem Training eines neuronalen Netzes. Je näher die Fehlerwerte bei Null liegen (hier: die orangefarbene vertikale Linie), desto besser ist die Leistung des Modells.

Nach dem Training werden die Ergebnisse des Netzes mit Hilfe eines Schwellenwerts und einer bedingten Aussage in zwei Klassen eingeteilt. $0.5$ ist der natürliche Schwellenwert, der sicherstellt, dass die gegebene Wahrscheinlichkeit, $1$ zu haben, größer ist als die Wahrscheinlichkeit, $0$ zu haben. Deshalb ist dies der Standard-Schwellenwert. Ausgabewerte oberhalb des Schwellenwerts werden mit $1$ und Werte unterhalb oder gleich dem Schwellenwert mit $0$ gekennzeichnet.

Schließlich konnte der Prozentsatz der richtigen Klassifizierungen berechnet werden.

und er entspricht $99.7\%$:

6. Anwendung

Nachdem das Netz trainiert und validiert wurde, kann das Netzobjekt verwendet werden, um die Reaktion des Netzes auf eine beliebige Eingabe zu berechnen; neue Daten oder aus dem geladenen Datensatz.

Im nächsten Codeausschnitt wird eine zufällige Pleuelstange aus dem Datensatz ausgewählt (hier: mit der Indexnummer $408$) und ihre Qualität wird vom trainierten Netz korrekt vorhergesagt (hier: Qualität 0=”OK”), wie in Abbildung 27 gezeigt: